题目内容
 如图(1)为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.
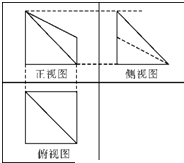
如图(1)为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.(1)如图(2)所示的方框内已给出了该几何体的俯视图,请在方框内画出该几何体的正(主)视图和侧(左)视图;并求四棱锥B-CEPD的体积;
(2)求证:BE∥平面PDA.
(3)求二面角P-AB-C的余弦值.
分析:(1)由已知中的直观图,结合“长对正,高平齐,宽相等”的原则,易画出几何体的三视图,结合已知及面面垂直的判定和性质,求出BC⊥平面PDCE,代入锥体体积公式可得四棱锥B-CEPD的体积;
(2)根据已知结合面面平行的判定定理可得平面EBC∥平面PDA,进而根据面面平行的性质定理,可得BE∥平面PDA.
(3)由已知易分析出∠PAD即为二面角P-AB-C的平面角,解三角形PAD即可得到二面角P-AB-C的余弦值.
(2)根据已知结合面面平行的判定定理可得平面EBC∥平面PDA,进而根据面面平行的性质定理,可得BE∥平面PDA.
(3)由已知易分析出∠PAD即为二面角P-AB-C的平面角,解三角形PAD即可得到二面角P-AB-C的余弦值.
解答:解:(1)该组合体的正视图和侧视图如下图所示.
∵PD⊥平面ABCD,PD?平面PDCE,
∴平面PDCE⊥平面ABCD.
∵BC⊥CD,
∴BC⊥平面PDCE.
∵S梯形PDCE=
(PD+EC)•DC=
×3×2=3,
∴四棱锥B-CEPD的体积为
VB-CEPD=
S梯形PDCE•BC=
×3×2=2.
证明:(2)∵EC∥PD,PD?平面PDA,EC?平面PDA,
∴EC∥平面PDA.同理,BC∥平面PDA.
∵EC?平面EBC,BC?平面EBC,且EC∩BC=C,
∴平面EBC∥平面PDA.
又∵BE?平面EBC,
∴BE∥平面PDA.
(3)∵PD⊥平面ABCD,
∴PD⊥AB
又∵底面ABCD为正方形
∴AD⊥AB
∴∠PAD即为二面角P-AB-C的平面角,
∵在Rt△PAD中,PD=AD
∴∠PAD=45°
则二面角P-AB-C的余弦值为

∵PD⊥平面ABCD,PD?平面PDCE,
∴平面PDCE⊥平面ABCD.
∵BC⊥CD,
∴BC⊥平面PDCE.
∵S梯形PDCE=
| 1 |
| 2 |
| 1 |
| 2 |
∴四棱锥B-CEPD的体积为
VB-CEPD=
| 1 |
| 3 |
| 1 |
| 3 |
证明:(2)∵EC∥PD,PD?平面PDA,EC?平面PDA,
∴EC∥平面PDA.同理,BC∥平面PDA.
∵EC?平面EBC,BC?平面EBC,且EC∩BC=C,
∴平面EBC∥平面PDA.
又∵BE?平面EBC,
∴BE∥平面PDA.
(3)∵PD⊥平面ABCD,
∴PD⊥AB
又∵底面ABCD为正方形
∴AD⊥AB
∴∠PAD即为二面角P-AB-C的平面角,
∵在Rt△PAD中,PD=AD
∴∠PAD=45°
则二面角P-AB-C的余弦值为
| ||
| 2 |
点评:本题考查直线与平面垂直的证明,考查平面与平面所成的锐二面角大小的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
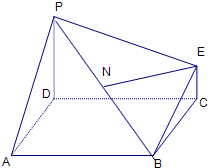 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC, 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC. 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.