题目内容
若函数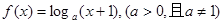 的定义域和值域都是[0,1],则a=( )
的定义域和值域都是[0,1],则a=( )
A. | B.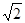 | C.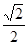 | D.2 |
D
解析试题分析:定义域是[0,1],故x+1∈[1,2]
又值域是[0,1],由于函数f(x)=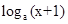 是一个单调函数,定义域左端点的函数值为0,故
是一个单调函数,定义域左端点的函数值为0,故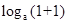 )=1,a=2,故答案为D
)=1,a=2,故答案为D
考点:对数函数的性质
点评:本题考查对数函数的性质,求解本题的关键是根据函数的性质及函数在一端点处的函数值为0判断出别一端点处的函数值为1,正确的判断很重要.

练习册系列答案
相关题目
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则
,则 ,在
,在 上所有零点之和为( )
上所有零点之和为( )
| A.7 | B.8 | C.9 | D.10 |
定义域为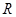 的函数
的函数 对任意
对任意 都有
都有 ,且其导函数
,且其导函数 满足
满足 ,则当
,则当 时,有( )
时,有( )
A. | B. |
C. | D. |
若定义在R上的偶函数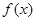 满足
满足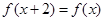 ,且当
,且当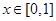 时,
时,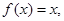 则方程
则方程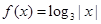 的解个数是 ( )
的解个数是 ( )
| A.0个 | B.2个 | C.4个 | D.6个 |
若函数 的定义域为
的定义域为 ,则实数a的取值范围为( )
,则实数a的取值范围为( )
A. | B.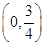 | C.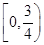 | D.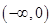 |
设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(1)=
| A.-3 | B.-1 | C.1 | D.3 |
已知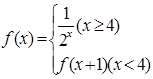 ,则
,则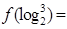 ( )
( )
A.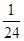 | B.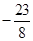 | C.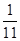 | D.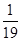 |
设函数 为定义在R上的奇函数,当
为定义在R上的奇函数,当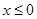 时,
时, (
( 为常数),则
为常数),则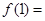 ( )
( )
| A.3 | B.1 | C.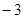 | D. |
若函数 在区间
在区间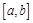 上为减函数,则
上为减函数,则 在
在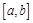 上( ).
上( ).
| A.至少有一个零点 | B.只有一个零点 |
| C.没有零点 | D.至多有一个零点 |