题目内容
给定下列命题:
①半径为2,圆心角的弧度数为
的扇形的面积为
;
②若a、β为锐角,tan(α+β)=
,tanβ=
则α+2β=
;
③若A、B是△ABC的两个内角,且sinA<sinB,则BC<AC;
④若a、b、c分别是△ABC的三个内角A、B、C所对边的长,且a2+b2-c2<0,则△ABC一定是钝角三角形.
其中真命题的序号是______.
①半径为2,圆心角的弧度数为
| 1 |
| 2 |
| 1 |
| 2 |
②若a、β为锐角,tan(α+β)=
| 1 |
| 3 |
| 1 |
| 2 |
| π |
| 4 |
③若A、B是△ABC的两个内角,且sinA<sinB,则BC<AC;
④若a、b、c分别是△ABC的三个内角A、B、C所对边的长,且a2+b2-c2<0,则△ABC一定是钝角三角形.
其中真命题的序号是______.
①由扇形的面积公式s=
=1故错误;②因为α+2β=(α+β)+β,则tan[(α+β)+β]=
=1,又因为α、β为锐角,所以
α+2β=
,故正确;③根据正弦定理得
=
,因为sinA<sinB,得到BC<AC故正确;④根据余弦定理得cosC=
,因为a2+b2-c2<0,而2ab>0,得到cosC<0,因为∠C∈(0,π)所以∠C为钝角故正确.
故答案为②③④
| nπr2 |
| 2π |
| tan(α+β)+tanβ |
| 1-tan(α+β)tanβ |
α+2β=
| π |
| 4 |
| BC |
| sinA |
| AC |
| sinB |
| a2+b2-c2 |
| 2ab |
故答案为②③④

练习册系列答案
相关题目
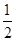 的扇形的面积为
的扇形的面积为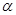 、
、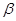 为锐角,
为锐角,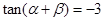 ,
,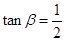 ,则
,则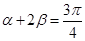 ;
;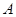 、
、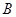 是△
是△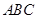 的两个内角,且
的两个内角,且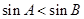 ,则
,则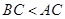 ;
;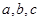 分别是△
分别是△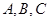 所对边的长,
所对边的长,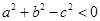 ,则△
,则△ 的扇形的面积为
的扇形的面积为 ;
;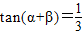 ,
,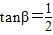 则
则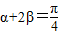 ;
; 的扇形的面积为
的扇形的面积为 ;
;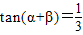 ,
,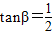 则
则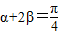 ;
;