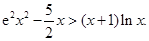题目内容
已知函数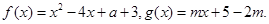
⑴当 时,若函数
时,若函数 存在零点,求实数
存在零点,求实数 的取值范围并讨论零点个数;
的取值范围并讨论零点个数;
⑵当 时,若对任意的
时,若对任意的 ,总存在
,总存在 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
【答案】
⑴实数a的取值范围是 .当
.当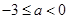 时,2个零点;当
时,2个零点;当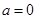 或
或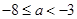 ,1个零点.
,1个零点.
⑵实数m的取值范围是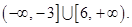
【解析】
试题分析:⑴可将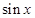 看作一个整体,令
看作一个整体,令 ,
,
所以问题转化为一个二次函数的问题,结合二次函数的图象即可得解.
⑵当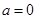 时,
时,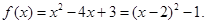 由此可得:
由此可得: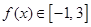 ,记
,记 .
.
对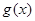 ,则分
,则分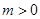 和
和 两种情况,求出
两种情况,求出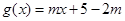 在
在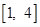 上的范围,这个范围为集合
上的范围,这个范围为集合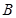 .因为对任意的
.因为对任意的 ,总存在
,总存在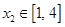 ,使
,使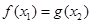 成立,所以
成立,所以 ,由此可得一不等式组,解这个不等式组即可得
,由此可得一不等式组,解这个不等式组即可得 的取值范围.
的取值范围.
试题解析:⑴令 ,
,
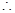 函数
函数 图象的对称轴为直线
图象的对称轴为直线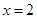 ,要使
,要使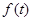 在
在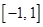 上有零点,
上有零点,
则 即
即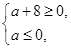

所以所求实数a的取值范围是 . 3分
. 3分
当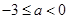 时,2个零点;当
时,2个零点;当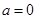 或
或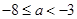 ,1个零点
7分
,1个零点
7分
⑵当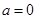 时,
时,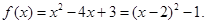
所以当 时,
时,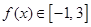 ,记
,记 .
.
由题意,知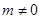 ,当
,当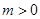 时,
时,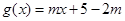 在
在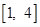 上是增函数,
上是增函数,
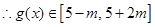 ,记
,记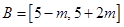 .
.
由题意,知
 解得
解得 9分
9分
当 时,
时,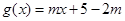 在
在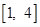 上是减函数,
上是减函数,
 ,记
,记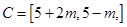 .
.
由题意,知
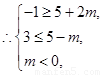 解得
解得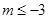 11分
11分
综上所述,实数m的取值范围是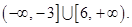 ..12分
..12分
考点:1、函数的零点;2、函数的最值;3、不等关系.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
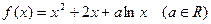 .
.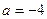 时,求
时,求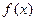 的最小值;
的最小值;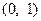 上为单调函数,求实数
上为单调函数,求实数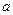 的取值范围;
的取值范围;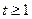 时,不等式
时,不等式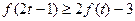 恒成立,求实数
恒成立,求实数 当
当 时,
时, 若在区间
若在区间 内,函数
内,函数 ,有三个不同的零点,则实数
,有三个不同的零点,则实数 的取值范围是( )
的取值范围是( ) B.
B.  C.
C. D.
D. 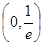
 .
.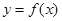 在点
在点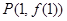 处的切线与直线
处的切线与直线 垂直,求函数
垂直,求函数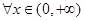 都有
都有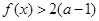 成立,试求
成立,试求 的取值范围;
的取值范围; .当
.当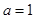 时,函数
时,函数 在区间
在区间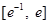 上有两个零点,求实数
上有两个零点,求实数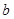 的取值范围.
的取值范围.
 在[1,2]上是减函数,求实数a的取值范围;
在[1,2]上是减函数,求实数a的取值范围; 是否存在实数a,当
是否存在实数a,当 (e是自然常数)时,函数
(e是自然常数)时,函数 的最小值是3,若存在,求出a的值;若不存在,说明理由;
的最小值是3,若存在,求出a的值;若不存在,说明理由;