题目内容
目前全世界都使用体重指数(BMI)来衡量一个人胖或不胖,计算的方法是:BMI=体重(kg)除以身高(m)的平方,世界卫生组织拟定的标准是:BMI在18.5-24.9时属正常范围,BMI大于25为超重,BMI大于30为肥胖,在某所高中随机抽取16名学生,测得身高、体重、BMI值如下表:表中身高单位为cm,体重单位为kg.
| 身高 | 166 | 169 | 170 | 166 | 180 | 175 | 177 | 176 |
| 体重 | 65 | 70 | 70 | 70 | 98 | 93 | 90 | 75 |
| BMI | 23.6 | 24.5 | 24.2 | 25.2 | 30.2 | 30.4 | 28.7 | 24.2 |
| 身高 | 174 | 182 | 181 | 168 | 169 | 185 | 181 | 179 |
| 体重 | 85 | 91 | 95 | 69 | 69 | 85 | 99 | 97 |
| BMI | 28.1 | 27.5 | 29 | 24.4 | 24.2 | 25 | 30.2 | 30.3 |
(Ⅱ)以这16人的样本数据来估计这所高中学校的整体数据,若从该校任选4人,ξ表示抽到肥胖学生的人数,求ξ的分布列及数学期望.
解:(I)根据信息可知,16人中有4个人肥胖,所以从这16人中随机选取4人,至多有一人是肥胖的概率为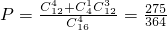 ;
;
(Ⅱ)任取1人,此人肥胖的概率为 ,故P(ξ=k)=
,故P(ξ=k)=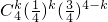 ,k=0,1,2,3,4
,k=0,1,2,3,4
∴分布列为
ξ的数学期望Eξ=0×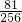 +1×
+1×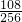 +2×
+2×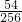 +3×
+3×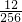 +4×
+4×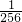 =1.
=1.
分析:(I)根据信息可知,16人中有4个人肥胖,利用等可能事件的概率公式,可求从这16人中随机选取4人,至多有一人是肥胖的概率;
(Ⅱ)任取1人,此人肥胖的概率为 ,故P(ξ=k)=
,故P(ξ=k)=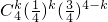 ,k=0,1,2,3,4,由此可得ξ的分布列及数学期望.
,k=0,1,2,3,4,由此可得ξ的分布列及数学期望.
点评:本题考查等可能事件的概率公式,考查离散型随机变量的分布列及数学期望,属于中档题.
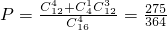 ;
;(Ⅱ)任取1人,此人肥胖的概率为
 ,故P(ξ=k)=
,故P(ξ=k)=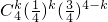 ,k=0,1,2,3,4
,k=0,1,2,3,4∴分布列为
| ξ | 0 | 1 | 2 | 3 | 4 |
| P | 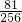 | 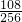 | 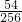 | 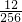 | 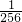 |
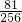 +1×
+1×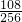 +2×
+2×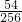 +3×
+3×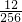 +4×
+4×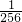 =1.
=1.分析:(I)根据信息可知,16人中有4个人肥胖,利用等可能事件的概率公式,可求从这16人中随机选取4人,至多有一人是肥胖的概率;
(Ⅱ)任取1人,此人肥胖的概率为
 ,故P(ξ=k)=
,故P(ξ=k)=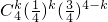 ,k=0,1,2,3,4,由此可得ξ的分布列及数学期望.
,k=0,1,2,3,4,由此可得ξ的分布列及数学期望.点评:本题考查等可能事件的概率公式,考查离散型随机变量的分布列及数学期望,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
目前全世界都使用体重指数(BMI)来衡量一个人胖或不胖,计算的方法是:BMI=体重(kg)除以身高(m)的平方,世界卫生组织拟定的标准是:BMI在18.5-24.9时属正常范围,BMI大于25为超重,BMI大于30为肥胖,在某所高中随机抽取16名学生,测得身高、体重、BMI值如下表:表中身高单位为cm,体重单位为kg.
(I)若从这16人中随机选取4人,求至多有一人是肥胖的概率;
(Ⅱ)以这16人的样本数据来估计这所高中学校的整体数据,若从该校任选4人,ξ表示抽到肥胖学生的人数,求ξ的分布列及数学期望.
| 身高 | 166 | 169 | 170 | 166 | 180 | 175 | 177 | 176 |
| 体重 | 65 | 70 | 70 | 70 | 98 | 93 | 90 | 75 |
| BMI | 23.6 | 24.5 | 24.2 | 25.2 | 30.2 | 30.4 | 28.7 | 24.2 |
| 身高 | 174 | 182 | 181 | 168 | 169 | 185 | 181 | 179 |
| 体重 | 85 | 91 | 95 | 69 | 69 | 85 | 99 | 97 |
| BMI | 28.1 | 27.5 | 29 | 24.4 | 24.2 | 25 | 30.2 | 30.3 |
(Ⅱ)以这16人的样本数据来估计这所高中学校的整体数据,若从该校任选4人,ξ表示抽到肥胖学生的人数,求ξ的分布列及数学期望.