题目内容
设A是单位圆x2+y2=1上的任意一点,i是过点A与x轴垂直的直线,D是直线i与x轴的交点,点M在直线l上,且满足丨DM丨=m丨DA丨(m>0,且m≠1).当点A在圆上运动时,记点M的轨迹为曲线C.(I)求曲线C的方程,判断曲线C为何种圆锥曲线,并求焦点坐标;
(Ⅱ)过原点且斜率为k的直线交曲线C于P、Q两点,其中P在第一象限,它在y轴上的射影为点N,直线QN交曲线C于另一点H,是否存在m,使得对任意的k>0,都有PQ⊥PH?若存在,求m的值;若不存在,请说明理由.
【答案】分析:(I)设M(x,y),A(x,y),根据丨DM丨=m丨DA丨,确定坐标之间的关系x=x,|y|= |y|,利用点A在圆上运动即得所求曲线C的方程;根据m∈(0,1)∪(1,+∞),分类讨论,可确定焦点坐标;
|y|,利用点A在圆上运动即得所求曲线C的方程;根据m∈(0,1)∪(1,+∞),分类讨论,可确定焦点坐标;
(Ⅱ)?x1∈(0,1),设P(x1,y1),H(x2,y2),则Q(-x1,-y1),N(0,y1),利用P,H两点在椭圆C上,可得 ,从而可得可得
,从而可得可得 .利用Q,N,H三点共线,及PQ⊥PH,即可求得结论.
.利用Q,N,H三点共线,及PQ⊥PH,即可求得结论.
解答:解:(I)如图1,设M(x,y),A(x,y)
∵丨DM丨=m丨DA丨,∴x=x,|y|=m|y|
∴x=x,|y|= |y|①
|y|①
∵点A在圆上运动,∴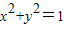 ②
②
①代入②即得所求曲线C的方程为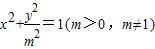
∵m∈(0,1)∪(1,+∞),
∴0<m<1时,曲线C是焦点在x轴上的椭圆,两焦点坐标分别为(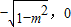 ),
),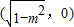
m>1时,曲线C是焦点在y轴上的椭圆,两焦点坐标分别为( ),
),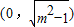
(Ⅱ)如图2、3,?x1∈(0,1),设P(x1,y1),H(x2,y2),则Q(-x1,-y1),N(0,y1),
∵P,H两点在椭圆C上,∴
①-②可得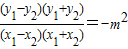 ③
③
∵Q,N,H三点共线,∴kQN=kQH,∴
∴kPQ•kPH=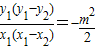
∵PQ⊥PH,∴kPQ•kPH=-1
∴
∵m>0,∴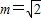
故存在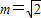 ,使得在其对应的椭圆
,使得在其对应的椭圆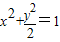 上,对任意k>0,都有PQ⊥PH
上,对任意k>0,都有PQ⊥PH
点评:本题考查轨迹方程,考查直线与椭圆的位置关系,考查代入法求轨迹方程,计算要小心.
 |y|,利用点A在圆上运动即得所求曲线C的方程;根据m∈(0,1)∪(1,+∞),分类讨论,可确定焦点坐标;
|y|,利用点A在圆上运动即得所求曲线C的方程;根据m∈(0,1)∪(1,+∞),分类讨论,可确定焦点坐标;(Ⅱ)?x1∈(0,1),设P(x1,y1),H(x2,y2),则Q(-x1,-y1),N(0,y1),利用P,H两点在椭圆C上,可得
 ,从而可得可得
,从而可得可得 .利用Q,N,H三点共线,及PQ⊥PH,即可求得结论.
.利用Q,N,H三点共线,及PQ⊥PH,即可求得结论.解答:解:(I)如图1,设M(x,y),A(x,y)
∵丨DM丨=m丨DA丨,∴x=x,|y|=m|y|
∴x=x,|y|=
 |y|①
|y|①∵点A在圆上运动,∴
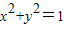 ②
②①代入②即得所求曲线C的方程为
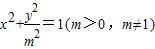
∵m∈(0,1)∪(1,+∞),
∴0<m<1时,曲线C是焦点在x轴上的椭圆,两焦点坐标分别为(
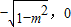 ),
),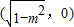
m>1时,曲线C是焦点在y轴上的椭圆,两焦点坐标分别为(
 ),
),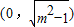
(Ⅱ)如图2、3,?x1∈(0,1),设P(x1,y1),H(x2,y2),则Q(-x1,-y1),N(0,y1),
∵P,H两点在椭圆C上,∴

①-②可得
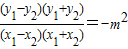 ③
③∵Q,N,H三点共线,∴kQN=kQH,∴

∴kPQ•kPH=
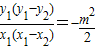
∵PQ⊥PH,∴kPQ•kPH=-1
∴

∵m>0,∴
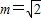
故存在
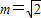 ,使得在其对应的椭圆
,使得在其对应的椭圆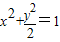 上,对任意k>0,都有PQ⊥PH
上,对任意k>0,都有PQ⊥PH
点评:本题考查轨迹方程,考查直线与椭圆的位置关系,考查代入法求轨迹方程,计算要小心.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目