Question

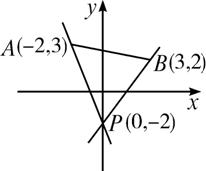
已知点A(-2，3)、B(3，2)、P(0，-2)，直线l过点P且与线段AB有公共点，用几何画板来演示此过程，并求l的斜率k的变化范围.

Answer 1

【探究】  如图，用几何画板来演示直线的变化过程，直线l是一簇绕点P转动而成的直线，点A和点B是它的两个极端位置.l以PB的位置逆时针转到PA的位置的过程中，其倾斜角从锐角α₁连续变大到钝角α₂，其斜率从tanα₁(正数)逐渐增大到+∞,又从-∞逐渐增大到tanα₂(负数).

同时，因为k_PB=,k_PA=,

且l与线段AB有公共点.

所以，斜率k的变化范围是(-∞,］∪［,+∞)

【规律总结】 本题是数形结合的思想方法在斜率中的应用，将直线l的转动与其斜率之间的变化联系起来，由“形”中观察l与AB有无交点，得到直线l的斜率变化范围，这是十分重要的一种数学方法.请认真体会.