题目内容
已知偶函数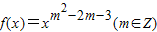 在(0,+∞)上单调递减.
在(0,+∞)上单调递减.(1)求函数f(x)的解析式;
(2)若f(2a+1)=f(a),求实数a的值.
【答案】分析:(1)由已知中函数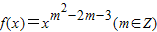 在(0,+∞)上单调递减,根据幂函数在(0,+∞)上的单调性与指数的关系,得到m2-2m-3<0,结合m∈Z,易函数f(x)为偶函数即m2-2m-3为偶数,我们易求出对应的m值,进而得到函数f(x)的解析式;
在(0,+∞)上单调递减,根据幂函数在(0,+∞)上的单调性与指数的关系,得到m2-2m-3<0,结合m∈Z,易函数f(x)为偶函数即m2-2m-3为偶数,我们易求出对应的m值,进而得到函数f(x)的解析式;
(2)由已知中函数f(x)为偶函数,我们可将f(2a+1)=f(a),转化为|2a+1|=|a|,根据绝对值的定义,解绝对值方程,即可得到答案.
解答:解:(1)由m2-2m-3<0得-1<m<3又m∈Z
∴m=0或1或2而m2-2m-3为偶数
∴m2-2m-3=-4,∴f(x)=x-4
(2)∵函数f(x)为偶函数,若f(2a+1)=f(a),
则|2a+1|=|a|,
即2a+1=a或2a+1=-a
∴a=-1或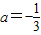 .
.
点评:本题考查的知识点是幂函数的性质,绝对值方程的解法,偶函数的性质,其中(1)的关键是熟练掌握幂函数的单调性,奇偶性,定义域与指数的关系,(2)的关键是利用偶函数的性质,将抽象方程,转化为绝对值方程.
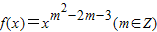 在(0,+∞)上单调递减,根据幂函数在(0,+∞)上的单调性与指数的关系,得到m2-2m-3<0,结合m∈Z,易函数f(x)为偶函数即m2-2m-3为偶数,我们易求出对应的m值,进而得到函数f(x)的解析式;
在(0,+∞)上单调递减,根据幂函数在(0,+∞)上的单调性与指数的关系,得到m2-2m-3<0,结合m∈Z,易函数f(x)为偶函数即m2-2m-3为偶数,我们易求出对应的m值,进而得到函数f(x)的解析式;(2)由已知中函数f(x)为偶函数,我们可将f(2a+1)=f(a),转化为|2a+1|=|a|,根据绝对值的定义,解绝对值方程,即可得到答案.
解答:解:(1)由m2-2m-3<0得-1<m<3又m∈Z
∴m=0或1或2而m2-2m-3为偶数
∴m2-2m-3=-4,∴f(x)=x-4
(2)∵函数f(x)为偶函数,若f(2a+1)=f(a),
则|2a+1|=|a|,
即2a+1=a或2a+1=-a
∴a=-1或
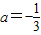 .
.点评:本题考查的知识点是幂函数的性质,绝对值方程的解法,偶函数的性质,其中(1)的关键是熟练掌握幂函数的单调性,奇偶性,定义域与指数的关系,(2)的关键是利用偶函数的性质,将抽象方程,转化为绝对值方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

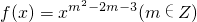 在(0,+∞)上单调递减.
在(0,+∞)上单调递减.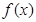 在区间[0,4]上是增函数, 则
在区间[0,4]上是增函数, 则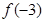 和
和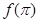 的大小关系是 ( )
的大小关系是 ( )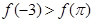 B.
B.
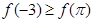
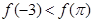 D.
无法确定
D.
无法确定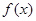 在区间
在区间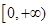 单调递增,则满足
单调递增,则满足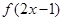 <
<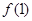 的
的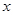 取值范围是( )
取值范围是( )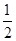 ,1) B.(
,1) B.(