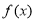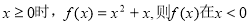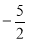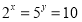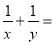题目内容
设函数 的定义域为
的定义域为 ,并且满足
,并且满足 ,且
,且 ,当
,当 时,
时,
(1).求 的值;(3分)
的值;(3分)
(2).判断函数 的奇偶性;(3分)
的奇偶性;(3分)
(3).如果 ,求
,求 的取值范围.(6分)
的取值范围.(6分)
(1)0;(2)函数 是奇函数;(3)
是奇函数;(3)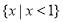 .
.
【解析】
试题分析:(1)令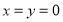 即可求出
即可求出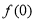 的值;
的值;
(2)由(1)知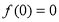 ,又有
,又有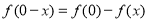 ,得
,得 ,又因为
,又因为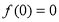 ,所以函数
,所以函数 是奇函数;
是奇函数;
(3)利用函数单调性的定义,结合 ,可得函数
,可得函数 的单调性,进而将抽象不等式转化为具体的不等式,即可求解.
的单调性,进而将抽象不等式转化为具体的不等式,即可求解.
试题解析:(1)令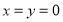 ,则
,则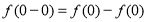 ,
,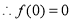 ;
;
(2)
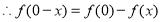
由(1)值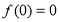 ,
,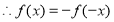
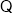
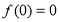
 函数
函数 是奇函数
是奇函数
(3)设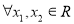 ,且
,且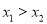 ,则
,则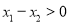 ,
,
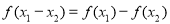
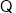 当
当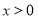 时,
时,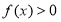
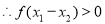 ,即
,即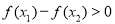
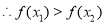
 函数
函数 是定义在
是定义在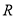 上的增函数
上的增函数

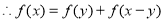
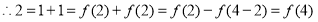
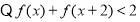
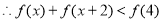
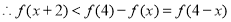
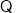 函数
函数 是定义在
是定义在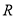 上的增函数
上的增函数
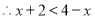
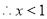
 不等式
不等式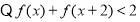 的解集为
的解集为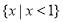
考点:1.抽象函数及其应用;2.函数的奇偶性的判断;3.函数单调性的性质.

练习册系列答案
相关题目
某射击俱乐部四名运动员甲、乙、丙、丁在选拔赛 中所得的平均环数 及其方差
及其方差 如表所示,若从中选送一人参加决赛,则最佳人选是
如表所示,若从中选送一人参加决赛,则最佳人选是
| 甲 | 乙 | 丙 | 丁 |
| 9.1 | 9.3 | 9.3 | 9.2 |
| 5.7 | 6.2 | 5.7 | 6.4 |
A.甲 B.乙
C.丙 D.丁