题目内容
放在衣柜里的樟脑丸,随着时间会挥发而体积缩小,刚放进的新丸体积为a,经过t天后体积与天数t的关系式为:V=a•e-kt,若新丸经过50天后,体积变为
a,那么经过几天后,体积变为
a?( )
| 4 |
| 9 |
| 8 |
| 27 |
分析:由题意,可得出V=a•e-50k=
a与V=a•e-kt=
a,两式作商求得e-(t-50)k=
,由于V=a•e-50k=
a可变为e-50k=
,对比e-(t-50)k=
,可得出2t-100=50,由此方程解出t的值即可选出正确选项
| 4 |
| 9 |
| 8 |
| 27 |
| 2 |
| 3 |
| 4 |
| 9 |
| 4 |
| 9 |
| 2 |
| 3 |
解答:解:由题意得V=a•e-50k=
a ①
可令t天后体积变为
a,即有V=a•e-kt=
a ②
由①可得e-50k=
③
又②÷①得e-(t-50)k=
,
两边平方得e-(2t-100)k=
,与③比较可得2t-100=50,解得t=75
即经过75天后,体积变为
a
故选C
| 4 |
| 9 |
可令t天后体积变为
| 8 |
| 27 |
| 8 |
| 27 |
由①可得e-50k=
| 4 |
| 9 |
又②÷①得e-(t-50)k=
| 2 |
| 3 |
两边平方得e-(2t-100)k=
| 4 |
| 9 |
即经过75天后,体积变为
| 8 |
| 27 |
故选C
点评:本题考点是指数函数综合题,考查了指数运算的综合,求解本题的关键是先待定t值为天数,建立起方程,再比较已知条件,得出t的方程,解出t值,本题解法巧妙,充分考虑了题设条件的特征,对观察判断能力要求较高,解题时根据题设条件选择恰当的方法可以大大降低计算量.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 a,那么经过22天后,体积变为
a,那么经过22天后,体积变为 ?( )
?( ) a,那么经过22天后,体积变为
a,那么经过22天后,体积变为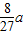 ?( )
?( ) a,那么经过22天后,体积变为
a,那么经过22天后,体积变为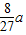 ?( )
?( )