题目内容
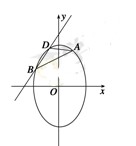
如图已知抛物线 :
: 过点
过点 ,直线
,直线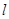 交
交 于
于 ,
, 两点,过点
两点,过点 且平行于
且平行于 轴的直线分别与直线
轴的直线分别与直线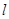 和
和 轴相交于点
轴相交于点 ,
, .
.
(1)求 的值;
的值;
(2)是否存在定点 ,当直线
,当直线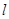 过点
过点 时,△
时,△ 与△
与△ 的面积相等?若存在,求出点
的面积相等?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(1)p=1;(2)详见解析.
解析试题分析:(1)因为 在抛物线C上,所以将点P坐标代入方程,即可求得p=1.
在抛物线C上,所以将点P坐标代入方程,即可求得p=1.
(2)先假设存在定点Q,设A(x1,y1),B(x2,y2),AB的方程为y=kx+b.联立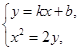 得
得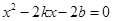 ,当
,当 时,有
时,有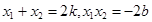 .由题意知,
.由题意知, ,
,
因为△PAM与△PBN的面积相等,所以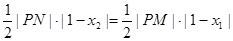 ,即
,即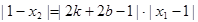 解得
解得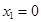 或
或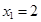 .所求的定点Q即为点A,即l过Q(0,0)或Q(2,2)时,满足条件..
.所求的定点Q即为点A,即l过Q(0,0)或Q(2,2)时,满足条件..
试题解析:(1)因为 在抛物线C上,所以1=2p·
在抛物线C上,所以1=2p·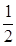 ,得p=1.
,得p=1.
(2)假设存在定点Q,设A(x1,y1),B(x2,y2),AB的方程为y=kx+b.
联立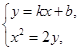 得
得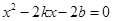 ,当
,当 时,有
时,有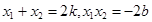 .
.
所以(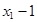 )(
)(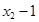 )=
)=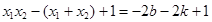 (*)由题意知,
(*)由题意知, ,
,
因为△PAM与△PBN的面积相等,所以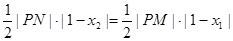 ,
,
即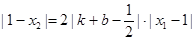 ,
,
也即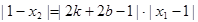
根据(*)式,得(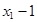 )2=1,解得
)2=1,解得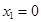 或
或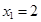 .
.
所求的定点Q即为点A,
即l过Q(0,0)或Q(2,2)时,满足条件.
考点:直线与抛物线的位置关系.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
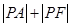 的最小值及此时P点的坐标.
的最小值及此时P点的坐标. 与抛物线
与抛物线 (常数
(常数 )相交于不同的两点
)相交于不同的两点 、
、 ,且
,且 (
( 为定值),线段
为定值),线段 的中点为
的中点为 ,与直线
,与直线 平行的切线的切点为
平行的切线的切点为 (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
 、
、 表示出
表示出 垂直于
垂直于 轴;
轴; 的面积,证明
的面积,证明 、
、 ,再作与
,再作与 、
、 ,小张马上写出了
,小张马上写出了 、
、 的面积,由此小张求出了直线
的面积,由此小张求出了直线 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
 ,点A、B在抛物线C上.
,点A、B在抛物线C上.
 =4p,求过A,B,O(O为坐标原点)三点的圆的方程;
=4p,求过A,B,O(O为坐标原点)三点的圆的方程; ,且
,且 ,问直线AB是否会过某一定点?若是,求出这一定点的坐标,若不是,请说明理由.
,问直线AB是否会过某一定点?若是,求出这一定点的坐标,若不是,请说明理由. 的中心为原点
的中心为原点 ,长轴在
,长轴在 轴上,离心率
轴上,离心率 ,又椭圆
,又椭圆 .
.
 轴的直线
轴的直线 与椭圆
与椭圆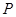 、
、 ,过
,过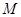 的圆,使椭圆
的圆,使椭圆 的面积
的面积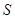 的最大值.
的最大值. 的离心率是
的离心率是 .
. ,使点C(2,0)关于直线
,使点C(2,0)关于直线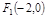 、
、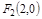 ,动点N满足
,动点N满足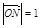 (O为坐标原点),
(O为坐标原点), ,
,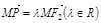 ,
,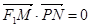 ,求点P的轨迹方程.
,求点P的轨迹方程. 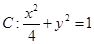 的上、下顶点分别为
的上、下顶点分别为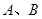 ,点
,点 在椭圆上,且异于点
在椭圆上,且异于点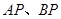 与直线
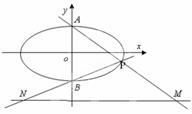
与直线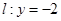 分别交于点
分别交于点 ,
,
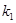 、
、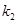 ,求证:
,求证: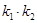 为定值;
为定值;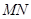 为直径的圆是否经过定点?请证明你的结论.
为直径的圆是否经过定点?请证明你的结论.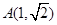 是离心率为
是离心率为 的椭圆
的椭圆 :
: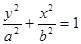
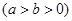 上的一点,斜率为
上的一点,斜率为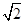 的直线
的直线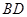 交椭圆
交椭圆 ,
,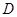 两点,且
两点,且 、
、
 ,
,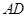 的斜率之和为定值.
的斜率之和为定值. .过点(m,0)作圆
.过点(m,0)作圆 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点. 表示为m的函数,并求
表示为m的函数,并求