题目内容
(本题12分)某校从参加高一年级期中考试的学生中随机抽出60名学生,将其数学成绩(均为整数)分成六段[40,50)、[50,60)、…、[90,100)后得到如下部分频率分布直方图.
观察图形的信息,回答下列问题:(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅲ)已知甲的考试成绩为45分,若从成绩在[40,60)的学生中随机抽取2人,求抽到学生甲的的概率.
观察图形的信息,回答下列问题:(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅲ)已知甲的考试成绩为45分,若从成绩在[40,60)的学生中随机抽取2人,求抽到学生甲的的概率.

(Ⅰ)频率分布直方图中纵坐标为0.003 ;
(Ⅱ)平均分为71 ;(Ⅲ)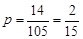
(Ⅱ)平均分为71 ;(Ⅲ)
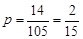
(I)根据每个区间上对应的矩形面积和为1,可以求出[70,80]上频率,进而求出纵坐标.
(2)平均分等于每个区间的中点值乘以此区间对应的矩形面积之和.
(3)先求出成绩在[40,60)的学生有0.25×60=15人,那么随机抽取2人有 105种方法,其中2人中含甲的有14种.然后根据古典概率计算公式计算即可.
105种方法,其中2人中含甲的有14种.然后根据古典概率计算公式计算即可.
解:(Ⅰ)设分数在[70,80)内的频率为x,根据频率分布直方图,有(0.01 + 0.015×2 + 0.025 + 0.005)×10 + x = 1,可得x=0.3,∴频率分布直方图中纵坐标为0.003 (频率3分,画图1分)
(Ⅱ)平均分为: =45´0.1+55´0.15+65´0.15+75´0.3 +85´0.25+95´0.05="71" ……8分
=45´0.1+55´0.15+65´0.15+75´0.3 +85´0.25+95´0.05="71" ……8分
(Ⅲ)因为成绩在[40,60)的学生有0.25×60=15人,从15人中随机抽取2人的情况共有1+2+3+…+14=105种,其中抽取到的2人中含甲的情况有14中,根据古典概型的计算公式,抽到甲的概率为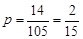 …………12分
…………12分
(2)平均分等于每个区间的中点值乘以此区间对应的矩形面积之和.
(3)先求出成绩在[40,60)的学生有0.25×60=15人,那么随机抽取2人有
 105种方法,其中2人中含甲的有14种.然后根据古典概率计算公式计算即可.
105种方法,其中2人中含甲的有14种.然后根据古典概率计算公式计算即可.解:(Ⅰ)设分数在[70,80)内的频率为x,根据频率分布直方图,有(0.01 + 0.015×2 + 0.025 + 0.005)×10 + x = 1,可得x=0.3,∴频率分布直方图中纵坐标为0.003 (频率3分,画图1分)
(Ⅱ)平均分为:
 =45´0.1+55´0.15+65´0.15+75´0.3 +85´0.25+95´0.05="71" ……8分
=45´0.1+55´0.15+65´0.15+75´0.3 +85´0.25+95´0.05="71" ……8分(Ⅲ)因为成绩在[40,60)的学生有0.25×60=15人,从15人中随机抽取2人的情况共有1+2+3+…+14=105种,其中抽取到的2人中含甲的情况有14中,根据古典概型的计算公式,抽到甲的概率为
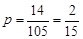 …………12分
…………12分
练习册系列答案
相关题目
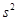 =
= 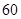 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段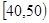 ,
,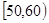 …
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: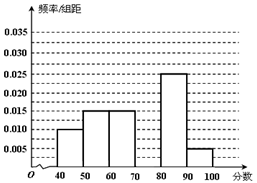
 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图; 的学生中抽取一个容量为
的学生中抽取一个容量为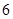 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取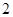 人,求至多有
人,求至多有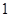 人在分数段
人在分数段 的概率.
的概率.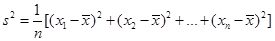 )
)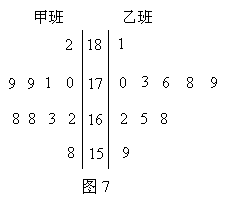
 对比班数学成绩的频数分布表:
对比班数学成绩的频数分布表:

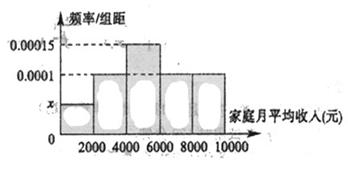
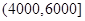 (元)间的每位同学得助学金1500元,家庭收入在
(元)间的每位同学得助学金1500元,家庭收入在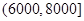 (元)间的每位同学得助学金1000元,家庭收入在
(元)间的每位同学得助学金1000元,家庭收入在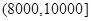 (元)间的同学不发助学金.
(元)间的同学不发助学金.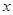 值;
值;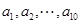 的平均数为
的平均数为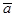 ,样本
,样本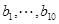 的平均数为
的平均数为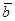 ,则样本
,则样本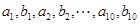 的平均数为( )
的平均数为( )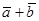

 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
, …
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图; 人,抽到的学生成绩在
人,抽到的学生成绩在 记
记 分,在
分,在 记
记 分,
分, 记
记 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求
 (单位:百万元)与销售额
(单位:百万元)与销售额 (单位:百万元)之间有如下数据:
(单位:百万元)之间有如下数据: