题目内容
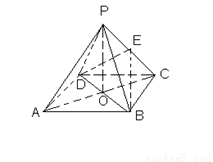
正四棱锥P-ABCD的五个顶点在同一球面上,若该四棱锥的底面边长为4,侧棱长为![]() ,则这个球的表面积为________.
,则这个球的表面积为________.
答案:36π
解析:
解析:
|
如图所示,取下底面正方形ABCD的中心O1,设球心为O,球半径为R,则PD= ∵O1O2+O1D2=OD2,∴(4-R)2+8=R2.解之,得R=3.∴S球=4πR2=36π.
|

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
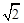 .M为线段PC的中点.
.M为线段PC的中点.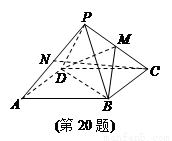
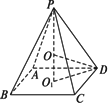
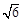 的正四棱锥P-ABCD内接于球O,则球面上A、B两点间的球面距离是
的正四棱锥P-ABCD内接于球O,则球面上A、B两点间的球面距离是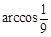 (B)
(B)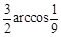 (C)
(C)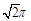 (D)
(D)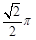
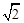 .M为线段PC的中点.
.M为线段PC的中点.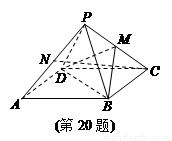
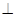 平面BDE
平面BDE