题目内容
在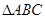 中,若
中,若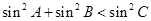 ,则
,则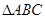 的形状是 ( )
的形状是 ( )
| A.钝角三角形 | B.直角三角形 | C.锐角三角形 | D.不能确定 |
A.
解析试题分析:由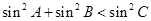 ,结合正弦定理可得,
,结合正弦定理可得,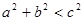 ,由余弦定理可得
,由余弦定理可得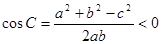 ,所以
,所以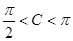 .所以
.所以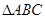 是钝角三角形.
是钝角三角形.
考点:余弦定理的应用;三角形的形状判断.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
钝角三角形ABC的面积是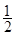 ,AB=1,BC=
,AB=1,BC= ,则AC=( )
,则AC=( )
| A.5 | B. | C.2 | D.1 |
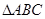 的内角
的内角 ,
, ,
, 的对边分别是
的对边分别是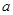 ,
,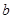 ,
,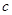 ,若
,若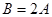 ,
, ,
,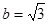 ,则
,则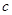 = ( )
= ( )
A.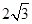 | B.2 | C.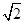 | D.1 |
在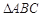 中,
中,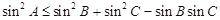 ,则
,则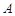 的取值范围是( )
的取值范围是( )
A.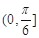 | B.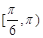 | C.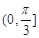 | D.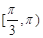 |
△ABC中,若 ,
,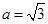 ,则
,则 等于 ( )
等于 ( )
A. | B. | C. | D.2 |
△ABC中,若 ,则△ABC的形状为( )
,则△ABC的形状为( )
| A.直角三角形 | B.等腰三角形 | C.等边三角形 | D.锐角三角形 |
在△ABC中,若最大角的正弦值是 ,则△ABC必是( )
,则△ABC必是( )
| A.等边三角形 | B.直角三角形 | C.钝角三角形 | D.锐角三角形 |
在△ABC中,已知a=1、b=2,C=120°,则c=( )
| A.3 | B.4 | C.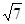 | D. |
在平行四边形ABCD中,对角线AC= ,BD=
,BD= ,周长为18,则这个平行四边形的面积为( )
,周长为18,则这个平行四边形的面积为( )
| A.16 | B. | C.18 | D.32 |