题目内容
已知函数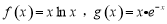 .
.
(1)记 ,求证:函数
,求证:函数 在区间
在区间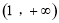 内有且仅有一个零点;
内有且仅有一个零点;
(2)用 表示
表示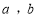 中的最小值,设函数
中的最小值,设函数 ,若关于
,若关于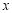 的方程
的方程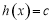 (其中
(其中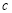 为常数)在区间
为常数)在区间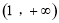 有两个不相等的实根
有两个不相等的实根 ,记
,记 在
在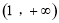 内的零点为
内的零点为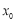 ,试证明:
,试证明: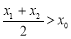 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知函数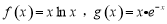 .
.
(1)记 ,求证:函数
,求证:函数 在区间
在区间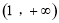 内有且仅有一个零点;
内有且仅有一个零点;
(2)用 表示
表示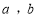 中的最小值,设函数
中的最小值,设函数 ,若关于
,若关于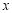 的方程
的方程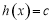 (其中
(其中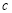 为常数)在区间
为常数)在区间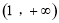 有两个不相等的实根
有两个不相等的实根 ,记
,记 在
在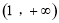 内的零点为
内的零点为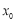 ,试证明:
,试证明: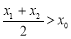 .
.
 阅读快车系列答案
阅读快车系列答案