题目内容
(本题满分12分) 商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少。把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元。现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的相同价格(标价)出售. 问:
(Ⅰ)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(Ⅱ)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
(Ⅰ)商场要获取最大利润,羊毛衫的标价应定为每件200元.
(Ⅱ),商场要获取最大利润的75%,每件标价为250元或150元.
解析试题分析:(Ⅰ)设购买人数为n人,羊毛衫的标价为每件x元,利润为y元,------1
则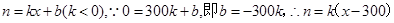 ------3
------3 ---4
---4
∵k<0,∴x=200时,ymax=" -" 10000k,--------------------------5
即商场要获取最大利润,羊毛衫的标价应定为每件200元. -------6
(Ⅱ)由题意得,k(x- 100)(x- 300)=" -" 10000k·75%----------7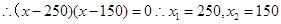 -----------------10
-----------------10
所以,商场要获取最大利润的75%,每件标价为250元或150元.------12
考点:本题主要考查函数模型,二次函数的性质的应用。
点评:典型题,作为实际应用问题,关键是理解题意,构建函数模型,即使实际问题数学化,利用数学知识求解。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
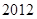 年中秋、国庆长假期间,由于国家实行
年中秋、国庆长假期间,由于国家实行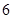 座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午
座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午 点,车辆通过该收费站的用时
点,车辆通过该收费站的用时 (分钟)与车辆到达该收费站的时刻
(分钟)与车辆到达该收费站的时刻 之间的函数关系式可近似地用以下函数给出:
之间的函数关系式可近似地用以下函数给出: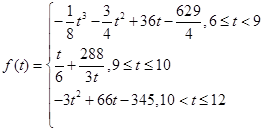
 万件、
万件、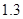 万件,为了估测当年每个月的产量,以这三个月的产品数量为依据,用一个函数模型模拟该产品的月产量
万件,为了估测当年每个月的产量,以这三个月的产品数量为依据,用一个函数模型模拟该产品的月产量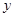 与月份
与月份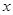 的关系,模拟函数可选用函数
的关系,模拟函数可选用函数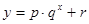 (其中
(其中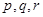 为常数)或二次函数。又已知当年4月份该产品的产量为
为常数)或二次函数。又已知当年4月份该产品的产量为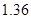 万件,请问用以上哪个函数作为模拟函数较好,并说明理由。
万件,请问用以上哪个函数作为模拟函数较好,并说明理由。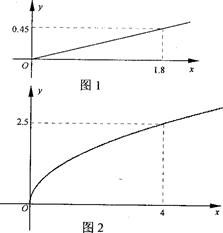
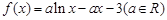 .
.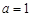 时,求函数
时,求函数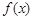 的单调区间;
的单调区间;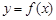 的图象在点
的图象在点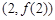 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的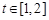 ,函数
,函数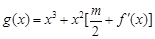 在区间
在区间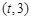 上总存在极值?
上总存在极值? 个月的利润
个月的利润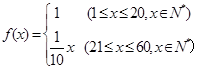 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第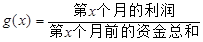 ,例如:
,例如: .
.  求
求 ; (Ⅱ)求第
; (Ⅱ)求第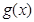 ;
; 的定义域为
的定义域为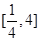 ,
,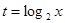 ,求
,求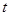 的取值范围;
的取值范围; 的最大值与最小值,并求出最值时对应的
的最大值与最小值,并求出最值时对应的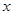 的值.
的值.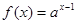 的图象经过点(2,
的图象经过点(2,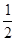 ),其中
),其中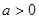 且
且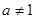 。
。 的值;
的值;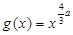 ,解关于
,解关于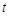 的不等式
的不等式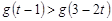 。
。 满足
满足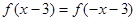 ,且该函数的图像与
,且该函数的图像与 轴交于点
轴交于点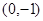 ,在
,在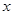 轴上截得的线段长为
轴上截得的线段长为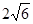 。
。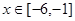 时,求
时,求