题目内容
定义：离心率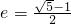
的椭圆为“黄金椭圆”，已知E：
（a＞b＞0）的一个焦点为F（c，0）（c＞0），则E为“黄金椭圆”是a，b，c成等比数列的
- A.既不充分也不必要条件
- B.充分且必要条件
- C.充分不必要条件
- D.必要不充分条件
B
分析：通过椭圆的离心率与a，b，c的关系，由黄金椭圆推出a，b，c是等比数列，再有a，b，c是等比数列，求出椭圆的离心率，即可判断椭圆是不是黄金椭圆，即可判断选项．
解答：对于黄金椭圆有c=a•e=a•
，b2=a2-c2=a2•=a•c，所以黄金椭圆的a．b．c必成等比数列，如果a．b．c成等比数列，所以b2=a2-c2=a•c，e2+e-1=0，解得，e=，所以椭圆是黄金椭圆；
所以E为“黄金椭圆”是a，b，c成等比数列的充分且必要条件．故选B．
点评：本题考查椭圆的基本性质，等比数列性质的应用，考查计算能力，充要条件的判断方法．
分析：通过椭圆的离心率与a，b，c的关系，由黄金椭圆推出a，b，c是等比数列，再有a，b，c是等比数列，求出椭圆的离心率，即可判断椭圆是不是黄金椭圆，即可判断选项．
解答：对于黄金椭圆有c=a•e=a•
，b2=a2-c2=a2•=a•c，所以黄金椭圆的a．b．c必成等比数列，如果a．b．c成等比数列，所以b2=a2-c2=a•c，e2+e-1=0，解得，e=，所以椭圆是黄金椭圆；所以E为“黄金椭圆”是a，b，c成等比数列的充分且必要条件．故选B．
点评：本题考查椭圆的基本性质，等比数列性质的应用，考查计算能力，充要条件的判断方法．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
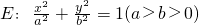的一个焦点为F（c，0）（c＞0），P为椭圆E上的任意一点．
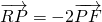？若存在，求直线l的斜率k；若不存在，请说明理由；
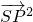取最大值时点P的坐标．
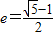的椭圆为“黄金椭圆”，已知椭圆
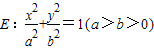的两个焦点分别为F1（-c，0）、F2（c，0）（c＞0），P为椭圆E上的任意一点．
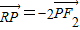？若存在，求直线l的斜率k；若不存在，请说明理由；
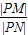的值．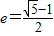
的椭圆为“黄金椭圆”，已知椭圆
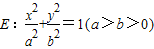的一个焦点为F（c，0）（c＞0），P为椭圆E上的任意一点．
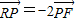？若存在，求直线l的斜率k；若不存在，请说明理由；
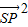取最大值时点P的坐标．
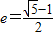的椭圆为“黄金椭圆”，已知椭圆E：
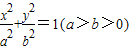的一个焦点为F（c，0），p为椭圆E上任意一点．
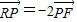；若存在，求直线l的斜率K；若不存在，说明理由．
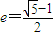的椭圆为“黄金椭圆”，已知E：
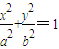（a＞b＞0）的一个焦点为F（c，0）（c＞0），则E为“黄金椭圆”是a，b，c成等比数列的（ ）