题目内容
设事件A发生的概率为p,证明事件A在一次试验中发生次数ξ的方差不超过1/4.
证明:∵ξ所有可能取的值为0,1.
P(ξ=0)=1-p,P(ξ=1)=p,
∴Eξ=0×(1-p)+1×p=p.
∴Dξ=(0-p)2×(1-p)+(1-p)2×p
=p(1-p)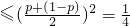 .
.
结论得证.
分析:事件A在一次试验中发生次数ξ的可能取值是0,1,根据事件A发生的概率p,写出事件A不发生的概率,表示出方差的表示式,化简整理,应用基本不等式求出最大值,结论得证.
点评:本题考查离散型随机变量的方差和基本不等式的应用,是一个综合题,考查同学们解题的能力,概率经常与其他的知识点组合.
P(ξ=0)=1-p,P(ξ=1)=p,
∴Eξ=0×(1-p)+1×p=p.
∴Dξ=(0-p)2×(1-p)+(1-p)2×p
=p(1-p)
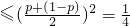 .
.结论得证.
分析:事件A在一次试验中发生次数ξ的可能取值是0,1,根据事件A发生的概率p,写出事件A不发生的概率,表示出方差的表示式,化简整理,应用基本不等式求出最大值,结论得证.
点评:本题考查离散型随机变量的方差和基本不等式的应用,是一个综合题,考查同学们解题的能力,概率经常与其他的知识点组合.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目