题目内容
已知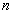 为正整数,试比较
为正整数,试比较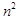 与
与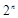 的大小 .
的大小 .
【答案】
当n=1时,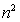 <
<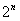 ;当n=2时,
;当n=2时,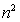 =
=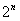 ; 当n=3时,
; 当n=3时,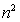 >
>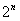 ; 当n=4时,
; 当n=4时,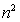 =
=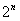 ;,当
;,当 时,
时,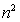 <
<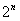
【解析】
试题分析:解:当n=1时,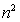 <
<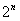 ; 1分
; 1分
当n=2时,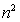 =
=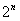 ; 2分
; 2分
当n=3时,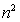 >
>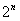 ;
3分
;
3分
当n=4时,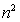 =
=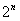 ;
4分
;
4分
当n=5时,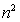 <
<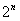 ; 当n=6时,
; 当n=6时,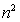 <
<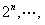
猜想:当 时,
时,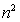 <
<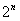 5分
5分
下面下面用数学归纳法证明:
(1)当n=5时,由上面的探求可知猜想成立 6分
(2)假设n=k(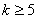 )时猜想成立,即
)时猜想成立,即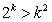 7分
7分
则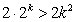 ,
,
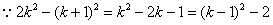 ,
,
当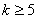 时
时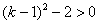
 ,从而
,从而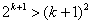
所以当n=k+1时,猜想也成立 9分
综合(1)(2),对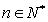 猜想都成立
10分
猜想都成立
10分
考点:数学归纳法
点评:对于不等式的证明可以通过通过对于n的讨论来得到,属于基础题。

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目