题目内容
设椭圆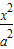 +
+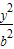 =1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
=1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.(1)求直线l和椭圆的方程;
(2)求证:点F1(-2,0)在以线段AB为直径的圆上;
(3)在直线l上有两个不重合的动点C、D,以CD为直径且过点F1的所有圆中,求面积最小的圆的半径长.
【答案】分析:(1)用点斜式写出直线的方程,由焦点坐标和准线方程求出椭圆的长半轴、短半轴的长,写出椭圆的方程.
(2)将直线方程代入椭圆方程,化为关于x的一元二次方程,利用根与系数的关系,计算x1+x2和x1x2的值,利用2个向量数量积公式计算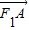 •
•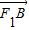 =0,得到F1A⊥F1B,所以点F1在以线段AB为直径的圆上.
=0,得到F1A⊥F1B,所以点F1在以线段AB为直径的圆上.
(3)面积最小的圆的半径长应是点F1到直线l的距离,用点到直线的距离公式求出圆的最小半径.
解答:解:(1)直线l:y=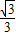 (x+3),
(x+3),
由已知c=2及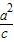 =3,解得a2=6,
=3,解得a2=6,
∴b2=6-22=2.
x2+3y2-6=0,①
∴椭圆方程为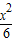 +
+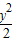 =1.
=1.
(2) y=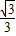 (x+3),②
(x+3),②
将②代入①,整理得2x2+6x+3=0.③
设A(x1,y1)、B(x2,y2),
则x1+x2=-3,x1x2= .
.
∵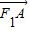 •
•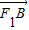 =(x1+2,y1)•(x2+2,y2)=(x1+2)(x2+2)+y1y2
=(x1+2,y1)•(x2+2,y2)=(x1+2)(x2+2)+y1y2
=x1x2+2(x1+x2)+4+ [x1x2+3(x1+x2)+9]=
[x1x2+3(x1+x2)+9]= x1x2+3(x1+x2)+7=0,
x1x2+3(x1+x2)+7=0,
∴F1A⊥F1B.则∠AF1B=90°.
∴点F1(-2,0)在以线段AB为直径的圆上.
(3)解:面积最小的圆的半径长应是点F1到直线l的距离,设为r.
∴r=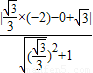 =
= 为所求.
为所求.
点评:本题考查求直线方程、椭圆的标准方程,直线和椭圆的位置关系.
(2)将直线方程代入椭圆方程,化为关于x的一元二次方程,利用根与系数的关系,计算x1+x2和x1x2的值,利用2个向量数量积公式计算
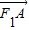 •
•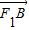 =0,得到F1A⊥F1B,所以点F1在以线段AB为直径的圆上.
=0,得到F1A⊥F1B,所以点F1在以线段AB为直径的圆上.(3)面积最小的圆的半径长应是点F1到直线l的距离,用点到直线的距离公式求出圆的最小半径.
解答:解:(1)直线l:y=
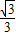 (x+3),
(x+3),由已知c=2及
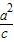 =3,解得a2=6,
=3,解得a2=6,∴b2=6-22=2.
x2+3y2-6=0,①
∴椭圆方程为
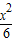 +
+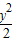 =1.
=1.(2) y=
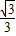 (x+3),②
(x+3),②将②代入①,整理得2x2+6x+3=0.③
设A(x1,y1)、B(x2,y2),
则x1+x2=-3,x1x2=
 .
.∵
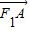 •
•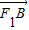 =(x1+2,y1)•(x2+2,y2)=(x1+2)(x2+2)+y1y2
=(x1+2,y1)•(x2+2,y2)=(x1+2)(x2+2)+y1y2=x1x2+2(x1+x2)+4+
 [x1x2+3(x1+x2)+9]=
[x1x2+3(x1+x2)+9]= x1x2+3(x1+x2)+7=0,
x1x2+3(x1+x2)+7=0,∴F1A⊥F1B.则∠AF1B=90°.
∴点F1(-2,0)在以线段AB为直径的圆上.
(3)解:面积最小的圆的半径长应是点F1到直线l的距离,设为r.
∴r=
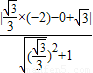 =
= 为所求.
为所求.点评:本题考查求直线方程、椭圆的标准方程,直线和椭圆的位置关系.

练习册系列答案
相关题目
 =1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
=1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为 .
. ;
; +
+ =1(a>b>0)的离心率为e,A为椭圆上一点,弦AB,AC分别过焦点F1,F2.
=1(a>b>0)的离心率为e,A为椭圆上一点,弦AB,AC分别过焦点F1,F2. =λ1
=λ1 ,
,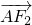 =λ2
=λ2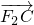 ,当A在椭圆上运动时,求证:λ1+λ2为定值.
,当A在椭圆上运动时,求证:λ1+λ2为定值.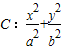 =1(a>b>0)过点
=1(a>b>0)过点 ,且左焦点为
,且左焦点为
 •
•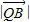 =
=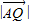 •
• ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上. =1(a>b>0)过点
=1(a>b>0)过点 ,且左焦点为
,且左焦点为
 •
• =
= •
• ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上. =1(a>b>0)的焦距为2c.以点O为圆心,a为半径作圆M.若过点P(
=1(a>b>0)的焦距为2c.以点O为圆心,a为半径作圆M.若过点P( ,0)所作圆M的两条切线互相垂直,则该椭圆的离心率为______
,0)所作圆M的两条切线互相垂直,则该椭圆的离心率为______