题目内容
在△ABC中，三个顶点的坐标分别是A（2，4），B（-1，2），C（1，0），点P（x，y）在△ABC内部运动，若点P满足
+2
+3
=
，则S△PAC：S△ABC=
| PA |
| PB |
| PC |
| 0 |
1：3
1：3
．分析：延长PB到B'，使PB'=2PB，延长PC到C'，使PC=3PC'，根据
+
+
=
可知P是△AB'C'的重心，然后设S△PAB'=S△PAC'=S△PB'C'=k，然后将三个三角形的面积用k表示，即可求出所求．
| PA |
| PB′ |
| PC’ |
| 0 |
解答：解：如图：延长PB到B'，使PB'=2PB，延长PC到C'，使PC=3PC'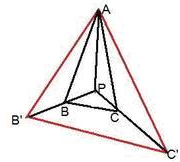
则
+
+
=
，P是△AB'C'的重心，
则S△PAB'=S△PAC'=S△PB'C'=k
S1=
S△PAB'=
k，S3=
S△PAC'=
k
S2=
PB×PC×sin∠BPC=
S△PB'C'=
k
故S1：S2：S3=
：
：
=3：1：2
∴S△PAC：S△ABC=1：3
故答案为：1：3
则
| PA |
| PB′ |
| PC’ |
| 0 |
则S△PAB'=S△PAC'=S△PB'C'=k
S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
S2=
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
故S1：S2：S3=
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
∴S△PAC：S△ABC=1：3
故答案为：1：3
点评：本题主要考查了向量在几何中的应用，以及
+
+
=
则P是△AB'C'的重心的应用，属于中档题．
| PA |
| PB′ |
| PC’ |
| 0 |
练习册系列答案
全能练考卷系列答案
相关题目
，则S△PAC：S△ABC= ．