题目内容
已知向量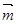
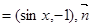
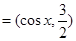 ,
,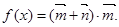
当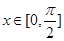 时,求函数
时,求函数 的值域:
的值域:
(2)锐角 中,
中,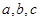 分别为角
分别为角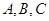 的对边,若
的对边,若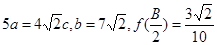 ,求边
,求边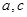 .
.
【答案】
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)先利用倍角公式、两角差的正弦公式将解析式化简,将已知 代入,求值域;(2)先通过第一问的解析式求出
代入,求值域;(2)先通过第一问的解析式求出 ,再通过凑角求出
,再通过凑角求出 ,用余弦定理求边.
,用余弦定理求边.
试题解析:(1) ,所以
,所以
 , 3分
, 3分
即
 ,
4分
,
4分
当 时,
时, ,
, ,
,
所以当 时,函数
时,函数 的值域是
的值域是 ;
6分
;
6分
(2)由 ,得
,得 ,又
,又 ,
,
所以 ,
8分
,
8分
因此 , 9分
, 9分
由余弦定理 ,得
,得 , 11分
, 11分
所以: 。
12分
。
12分
考点:1.三角函数式的化简;2.降幂公式;3.余弦定理.

练习册系列答案
相关题目
 ,设
,设 ,当
,当 时,不等式
时,不等式 恒成立.求实数
恒成立.求实数 的范围.
的范围.