Question

已知O为直角坐标系原点，P，Q坐标均满足不等式组

4x+3y-25≤0 x-2y+2≤0 x-1≥0

，则使cos∠POQ取最小值时的∠POQ的大小为（　　）

• A．

  π

  2

• B．π
• C．2π
• D．

  π

  4

Answer 1

分析：画出不等式组式组

4x+3y-25≤0 x-2y+2≤0 x-1≥0

，对应的平面区域，利用余弦函数在[0，π]上是减函数，再找到∠POQ最大时对应的点的坐标，就可求出cos∠POQ的最小值

解答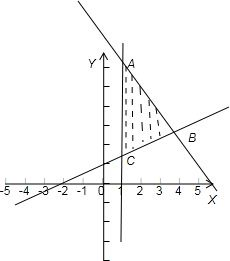：解：作出满足不等式组

4x+3y-25≤0 x-2y+2≤0 x-1≥0

，
因为余弦函数在[0，π]上是减函数，所以角最大时对应的余弦值最小，
由图得，当P与A（7，1）重合，Q与B（4，3）重合时，∠POQ最大．
此时k_OB=

3

4

，k_0A=7．
由tan∠POQ=

7- 3 4

1+7× 3 4

=1
∴∠POQ=

π

4

故选D

点评：本题属于线性规划中的拓展题，对于可行域不要求线性目标函数的最值，而是求可行域内的点与原点（0，0）围成的角的问题，注意夹角公式的应用．