题目内容
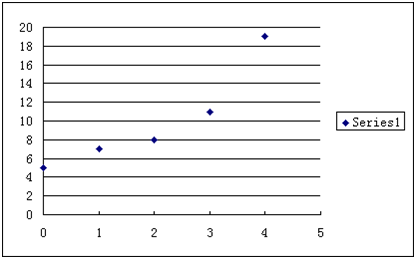
某城市理论预测2000年到2004年人口总数与年份的关系如下表所示| 年份200x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数y(十)万 | 5 | 7 | 8 | 11 | 19 |
(2)请根据上表提供的数据,利用最小二乘法求出y关于x的线性回归方程y=bx+a;
(3)据此估计2010年,该城市人口总数.(参考数值:0×5+1×7+2×8+3×11+4×19=132,02+12+22+32+42=30,公式见卷首)
分析:(1)根据所给的五对数据作为点的坐标,在坐标系中画出对应的点,得到散点图.
(2)先求出五对数据的平均数,做出横标和纵标的平均数,得到样本中心点,把所给的数据代入公式,利用最小二乘法求出线性回归方程的系数,再求出a的值,得到线性回归方程.
(3)把x=10代入线性回归方程,得到y=35.6,即2010年该城市人口数大约为35.6(十万)
(2)先求出五对数据的平均数,做出横标和纵标的平均数,得到样本中心点,把所给的数据代入公式,利用最小二乘法求出线性回归方程的系数,再求出a的值,得到线性回归方程.
(3)把x=10代入线性回归方程,得到y=35.6,即2010年该城市人口数大约为35.6(十万)
解答:(1)根据所给的五对数据作为点的坐标,在坐标系中画出对应的点,得到散点图.
(2)
=2,
=10
∵b=
=3.2
∴10=3.2×2+a,
∴a=3.6
∴回归直线方程为y=3.2x+3.6
(3)把x=10代入线性回归方程,得到y=35.6
即2010年该城市人口数大约为35.6(十万)

(2)
. |
| x |
. |
| y |
∵b=
| 132-5×2×10 |
| 30-5×4 |
∴10=3.2×2+a,
∴a=3.6
∴回归直线方程为y=3.2x+3.6
(3)把x=10代入线性回归方程,得到y=35.6
即2010年该城市人口数大约为35.6(十万)
点评:本题考查线性回归方程的求法和应用,本题解题的关键是正确利用最小二乘法公式,写出正确结果,注意在求预报值时,代入的自变量是10.

练习册系列答案
相关题目
(本小题满分10分)
某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
|
年份200x(年) |
0 |
1 |
2 |
3 |
4 |
|
人口数 y (十万) |
5 |
7 |
8 |
11 |
19 |
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,用最小二乘法求出 y 关于x的线性回归方程;
(Ⅲ)据此估计2005年该城市人口总数。
参考数值:0×5+1×7+2×8+3×11+4×19=132, ,
,
参考公式: 用最小二乘法求线性回归方程系数公式 
某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
|
年份200x(年) |
0 |
1 |
2 |
3 |
4 |
|
人口数 y (十万) |
5 |
7 |
8 |
11 |
19 |
根据表格和线性回归方程,可预报在2005年,该城市人口总数是___________
( 参考数值:0×5+1×7+2×8+3×11+4×19=132,
 ,公式见卷首 )
,公式见卷首 )
某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
|
年份200x(年) |
0 |
1 |
2 |
3 |
4 |
|
人口数y(十)万 |
5 |
7 |
8 |
11 |
19 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求出Y关于x的线性回归方程Y=bx+a;
(3)据此估计2005年.该 城市人口总数。