题目内容
已知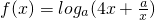 在区间[1,2]上为增函数,则a的取值范围是________.
在区间[1,2]上为增函数,则a的取值范围是________.
(1,4]
分析:把函数f(x)分解为两个基本函数y=logat与t=4x+ ,因为f(x)在区间[1,2]上为增函数,所以两函数y=logat与t=4x+
,因为f(x)在区间[1,2]上为增函数,所以两函数y=logat与t=4x+ 须同增或同减,
须同增或同减,
分a>1与0<a<1两种情况讨论再利用导数即可得到答案.
解答: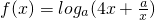 可看作由y=logat与t=4x+
可看作由y=logat与t=4x+ 复合而成的,x∈[1,2]时,4x
复合而成的,x∈[1,2]时,4x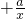 >0.
>0.
①当a>1时,y=logat单调递增,因为f(x)单调递增,则须有t=4x+ ,x∈[1,2],单调递增,
,x∈[1,2],单调递增,
所以t′=4- ≥0即a≤4x2在x∈[1,2]上恒成立,所以a≤4×12=4,则1<a≤4;
≥0即a≤4x2在x∈[1,2]上恒成立,所以a≤4×12=4,则1<a≤4;
②当时,y=logat单调递减,因为f(x)单调递增,则须有t=4x+ ,x∈[1,2],单调递减,
,x∈[1,2],单调递减,
所以t′=4- ≤0即a≥4x2在x∈[1,2]上恒成立,所以a≥4×22=16,与0<a<1矛盾.
≤0即a≥4x2在x∈[1,2]上恒成立,所以a≥4×22=16,与0<a<1矛盾.
综上,a的取值范围是(1,4].
故答案为:(1,4].
点评:本题考查复合函数单调性的判断问题,应注意其判断方法:同增异减.
分析:把函数f(x)分解为两个基本函数y=logat与t=4x+
 ,因为f(x)在区间[1,2]上为增函数,所以两函数y=logat与t=4x+
,因为f(x)在区间[1,2]上为增函数,所以两函数y=logat与t=4x+ 须同增或同减,
须同增或同减,分a>1与0<a<1两种情况讨论再利用导数即可得到答案.
解答:
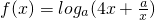 可看作由y=logat与t=4x+
可看作由y=logat与t=4x+ 复合而成的,x∈[1,2]时,4x
复合而成的,x∈[1,2]时,4x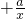 >0.
>0.①当a>1时,y=logat单调递增,因为f(x)单调递增,则须有t=4x+
 ,x∈[1,2],单调递增,
,x∈[1,2],单调递增,所以t′=4-
 ≥0即a≤4x2在x∈[1,2]上恒成立,所以a≤4×12=4,则1<a≤4;
≥0即a≤4x2在x∈[1,2]上恒成立,所以a≤4×12=4,则1<a≤4;②当时,y=logat单调递减,因为f(x)单调递增,则须有t=4x+
 ,x∈[1,2],单调递减,
,x∈[1,2],单调递减,所以t′=4-
 ≤0即a≥4x2在x∈[1,2]上恒成立,所以a≥4×22=16,与0<a<1矛盾.
≤0即a≥4x2在x∈[1,2]上恒成立,所以a≥4×22=16,与0<a<1矛盾.综上,a的取值范围是(1,4].
故答案为:(1,4].
点评:本题考查复合函数单调性的判断问题,应注意其判断方法:同增异减.

练习册系列答案
相关题目