题目内容
已知直线l的斜率为6,且被两坐标轴所截得的线段长为| 37 |
分析:斜截式设出直线方程,求出它与两坐标轴的交点坐标,利用被两坐标轴所截得的线段长为
,解出待定系数,即得直线l的方程.
| 37 |
解答:解:设直线l的方程 y=6x+b,它与两坐标轴的交点(0,b),(-
,0),
则b2+
=37,∴b2=36,b=±6,
∴所求的直线l的方程为 6x-y±6=0.
| b |
| 6 |
则b2+
| b2 |
| 36 |
∴所求的直线l的方程为 6x-y±6=0.
点评:本题考查用待定系数法求直线的斜截式方程,以及直线在两坐标轴上的截距的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
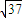 ,求直线l的方程.
,求直线l的方程.