题目内容
已知双曲线的一条渐近线方程为y=
x,且其中一个焦点坐标为(
,0)
(1)求双曲线的方程.
(2)若直线y-ax-1=0与该双曲线交于A、B两点,当a为何值时,A、B在双曲线的同一支上?
| 3 |
2
| ||
| 3 |
(1)求双曲线的方程.
(2)若直线y-ax-1=0与该双曲线交于A、B两点,当a为何值时,A、B在双曲线的同一支上?
分析:(1)先由双曲线的渐近线方程为y=
x,可假设方程为:x2-
=λ(λ>0),再由焦点为(
,0)可得双曲线的标准方程.
(2)在方程组
中消去y得,(3-a2)x2-2ax-2=0.依题意知该方程有两相异实根,且两根同号.从而可建立不等关系,故可解.
| 3 |
| y2 |
| 3 |
2
| ||
| 3 |
(2)在方程组
|
解答:解:(1)由题意知 C=
且焦点在x轴上,
又∵双曲线的一条渐近线方程为y=
x,
不妨令双曲线方程为:x2-
=λ(λ>0),
易知:a2=λb2=3λ,∴c2=4λ=
,
解得λ=
,
∴双曲线方程为:
-y=1,即 3x2-y=1…(6分)
(2)由
消去y知:(3-a2)x2-2ax-2=0,
依题意知该方程有两相异实根,且两根同号∴
解得:3<a2<6,即 -
<a<-
或
<a<
综上知:a∈(-
,-
)∪(
,
)…(12分)
2
| ||
| 3 |
又∵双曲线的一条渐近线方程为y=
| 3 |
不妨令双曲线方程为:x2-
| y2 |
| 3 |
易知:a2=λb2=3λ,∴c2=4λ=
| 4 |
| 3 |
解得λ=
| 1 |
| 3 |
∴双曲线方程为:
| x2 | ||
|
(2)由
|
依题意知该方程有两相异实根,且两根同号∴
|
解得:3<a2<6,即 -
| 6 |
| 3 |
| 3 |
| 6 |
综上知:a∈(-
| 6 |
| 3 |
| 3 |
| 6 |
点评:本题的考点是直线与圆锥曲线的综合,主要考查考查双曲线的标准方程,考查圆锥曲线的性质和应用,解题时要认真审题,注意等价转化.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
 -
- =1(a>0,b>0)的左顶点,且此双曲线的一条渐
=1(a>0,b>0)的左顶点,且此双曲线的一条渐 B.2
B.2 D.2
D.2 分别是双曲线
分别是双曲线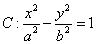
 的左,右焦点。过点
的左,右焦点。过点 与双曲线的一条渐
与双曲线的一条渐 ,且
,且 ,则双曲线的离心率为( )
,则双曲线的离心率为( ) (B)
(B) 
 (D)
(D)
