题目内容
在△ABC中,角A的对边长等于2,向量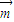 =
=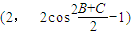 ,向量
,向量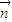 =
=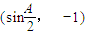 .
.(1)求
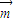 •
•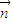 取得最大值时的角A的大小;
取得最大值时的角A的大小;(2)在(1)的条件下,求△ABC面积的最大值.
【答案】分析:(1)根据平面向量的数量积的运算法则求出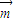 •
•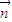 ,然后根据三角形的内角和定理,利用二倍角的余弦函数公式化简后进行配方得到
,然后根据三角形的内角和定理,利用二倍角的余弦函数公式化简后进行配方得到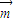 •
•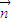 =-2
=-2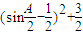 ,由
,由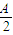 为锐角,利用二次函数求最值得到
为锐角,利用二次函数求最值得到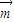 •
•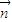 取最小值时sin
取最小值时sin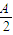 =
= ,根据特殊角的三角函数值求出A即可;
,根据特殊角的三角函数值求出A即可;
(2)由a=2,根据第一问求得cosA的值,利用余弦定理和基本不等式求出bc的最大值,根据S△ABC= bcsinA=
bcsinA=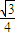 bc,把bc的最大值代入到面积公式里得到面积的最大值.
bc,把bc的最大值代入到面积公式里得到面积的最大值.
解答:解:(1) •
•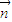 =2
=2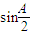 -
-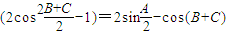 .
.
因为A+B+C=π,所以B+C=π-A,
于是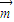 •
•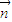 =
=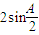 +cosA=-2
+cosA=-2 =-2
=-2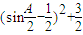 .
.
因为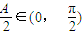 ,所以当且仅当
,所以当且仅当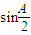 =
= ,即A=
,即A= 时,
时,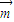 •
•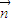 取得最大值
取得最大值 .
.
故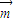 •
•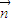 取得最大值时的角A=
取得最大值时的角A=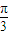 ;
;
(2)设角、B、C所对的边长分别为a、b、c由余弦定理,得b2+c2-a2=2bccosA
即bc+4=b2+c2≥2bc,所以bc≤4,当且仅当b=c=2时取等号.
又S△ABC= bcsinA=
bcsinA=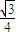 bc≤
bc≤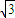 .当且仅当a=b=c=2时,△ABC的面积最大为
.当且仅当a=b=c=2时,△ABC的面积最大为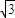 .
.
点评:考查学生会进行平面向量的数量积的运算,灵活运用二次函数求值的方法及灵活运用余弦定理化简求值.会利用基本不等式求最值.
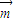 •
•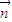 ,然后根据三角形的内角和定理,利用二倍角的余弦函数公式化简后进行配方得到
,然后根据三角形的内角和定理,利用二倍角的余弦函数公式化简后进行配方得到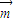 •
•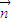 =-2
=-2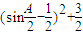 ,由
,由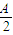 为锐角,利用二次函数求最值得到
为锐角,利用二次函数求最值得到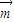 •
•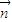 取最小值时sin
取最小值时sin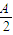 =
= ,根据特殊角的三角函数值求出A即可;
,根据特殊角的三角函数值求出A即可;(2)由a=2,根据第一问求得cosA的值,利用余弦定理和基本不等式求出bc的最大值,根据S△ABC=
 bcsinA=
bcsinA=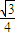 bc,把bc的最大值代入到面积公式里得到面积的最大值.
bc,把bc的最大值代入到面积公式里得到面积的最大值.解答:解:(1)
 •
•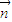 =2
=2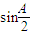 -
-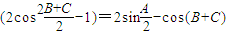 .
.因为A+B+C=π,所以B+C=π-A,
于是
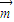 •
•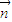 =
=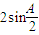 +cosA=-2
+cosA=-2 =-2
=-2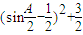 .
.因为
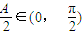 ,所以当且仅当
,所以当且仅当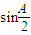 =
= ,即A=
,即A= 时,
时,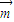 •
•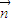 取得最大值
取得最大值 .
.故
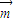 •
•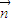 取得最大值时的角A=
取得最大值时的角A=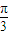 ;
;(2)设角、B、C所对的边长分别为a、b、c由余弦定理,得b2+c2-a2=2bccosA
即bc+4=b2+c2≥2bc,所以bc≤4,当且仅当b=c=2时取等号.
又S△ABC=
 bcsinA=
bcsinA=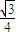 bc≤
bc≤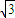 .当且仅当a=b=c=2时,△ABC的面积最大为
.当且仅当a=b=c=2时,△ABC的面积最大为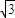 .
.点评:考查学生会进行平面向量的数量积的运算,灵活运用二次函数求值的方法及灵活运用余弦定理化简求值.会利用基本不等式求最值.

练习册系列答案
相关题目
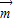 =
=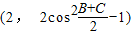 ,向量
,向量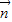 =
=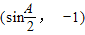 .
.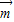 •
•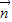 取得最大值时的角A的大小;
取得最大值时的角A的大小;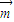 =
=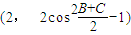 ,向量
,向量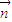 =
=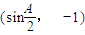 .
.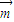 •
•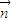 取得最大值时的角A的大小;
取得最大值时的角A的大小;