题目内容
已知lg3，lg（sinx-
），lg（1-y）顺次成等差数列，则（ ）A．y有最小值
，无最大值B．y有最大值1，无最小值
C．y有最小值
，最大值1D．y有最小值-1，最大值1
【答案】分析：先由等差中项来构造函数，再将sinx换元将函数转化为二次函数求最值．
解答：解：∵lg3，lg（sinx-
），lg（1-y）顺次成等差数列，
∴2lg（sinx-
）=lg3+lg（1-y）
∴
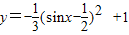
又sinx-
＞0，1-y＞0
∴y有最小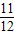值
，无最大值
故选A
点评：本题主要是数列作为一个载体来考查函数求最值问题．
解答：解：∵lg3，lg（sinx-
），lg（1-y）顺次成等差数列，∴2lg（sinx-
）=lg3+lg（1-y）∴
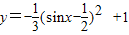
又sinx-
＞0，1-y＞0∴y有最小值
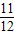，无最大值故选A
点评：本题主要是数列作为一个载体来考查函数求最值问题．
练习册系列答案
相关题目
已知lg3，lg（sinx-
），lg（1-y）顺次成等差数列，则（ ）
| 1 |
| 2 |
A、y有最小值
| ||
| B、y有最大值1，无最小值 | ||
C、y有最小值
| ||
| D、y有最小值-1，最大值1 |
），lg（1-y）顺次成等差数列，则（ ）
，无最大值
，最大值1
），lg（1-y）顺次成等差数列，则（ ）
，无最大值
，最大值1
），lg（1-y）顺次成等差数列，则（ ）
，无最大值
，最大值1