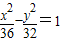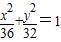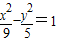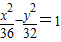题目内容
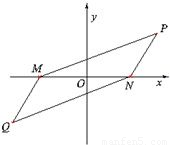
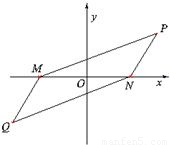
某荒漠上有相距4km的M,N两点,要围垦出以MN为一条对角线的平行四边形区域,建成农艺园.按照规划,围墙总长为12km.在设计图纸上,建立平面直角坐标系如图(O为MN的中点),那么平行四边形另外两个顶点P,Q的坐标满足的方程是 .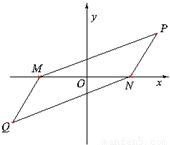
【答案】分析:由题意可得 PM+PN=6>MN=4,故点P的轨迹是以M,N为焦点的椭圆,根据已知中M,N两点相距4km,围墙总长为12km,可得a=3,c=2,进而根据椭圆标准方程的定义,可求得点P的轨迹方程,从而得到结论.
解答:解:由题意可得 PM+PN=6>MN=4,故点P的轨迹是以M,N为焦点的椭圆,
又∵M,N两点相距4km,围墙总长为12km,
∴a=3,c=2,
∴b=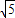 ,
,
故椭圆的方程为 . 同理,点Q的轨迹也是此椭圆,
. 同理,点Q的轨迹也是此椭圆,
故答案为: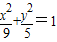 .
.
点评:点评:本题考查椭圆的定义、标准方程,根据椭圆的定义判断点P的轨迹是以M,N为焦点的椭圆,是解题的关键.
解答:解:由题意可得 PM+PN=6>MN=4,故点P的轨迹是以M,N为焦点的椭圆,
又∵M,N两点相距4km,围墙总长为12km,
∴a=3,c=2,
∴b=
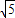 ,
,故椭圆的方程为
 . 同理,点Q的轨迹也是此椭圆,
. 同理,点Q的轨迹也是此椭圆,故答案为:
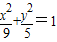 .
.点评:点评:本题考查椭圆的定义、标准方程,根据椭圆的定义判断点P的轨迹是以M,N为焦点的椭圆,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
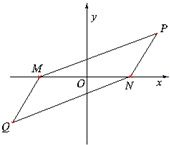 某荒漠上有相距4km的M,N两点,要围垦出以MN为一条对角线的平行四边形区域,建成农艺园.按照规划,围墙总长为12km.在设计图纸上,建立平面直角坐标系如图(O为MN的中点),那么平行四边形另外两个顶点P,Q的坐标满足的方程是( )
某荒漠上有相距4km的M,N两点,要围垦出以MN为一条对角线的平行四边形区域,建成农艺园.按照规划,围墙总长为12km.在设计图纸上,建立平面直角坐标系如图(O为MN的中点),那么平行四边形另外两个顶点P,Q的坐标满足的方程是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
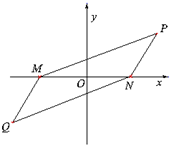 某荒漠上有相距4km的M,N两点,要围垦出以MN为一条对角线的平行四边形区域,建成农艺园.按照规划,围墙总长为12km.在设计图纸上,建立平面直角坐标系如图(O为MN的中点),那么平行四边形另外两个顶点P,Q的坐标满足的方程是
某荒漠上有相距4km的M,N两点,要围垦出以MN为一条对角线的平行四边形区域,建成农艺园.按照规划,围墙总长为12km.在设计图纸上,建立平面直角坐标系如图(O为MN的中点),那么平行四边形另外两个顶点P,Q的坐标满足的方程是