题目内容
已知b函数f(x)=
,x∈[1,∞).
(1)当a<0时,判断函数f(x)的单调性,并证明你的结论;
(3)当a=
时,求函数f(x)的最值.
| x2+2x+a |
| x |
(1)当a<0时,判断函数f(x)的单调性,并证明你的结论;
(3)当a=
| 1 |
| 2 |
(1)当a<0时,函数f(x)是[1,+∞)单调增函数.(1分)
证明:任取x1,x2∈[1,+∞)且x1<x2,则
f(x1)-f(x2)=
-
=
,(4分)
∵x1,x2∈[1,+∞)且x1<x2,a<0
∴
<0,(6分)
∴f(x1)<f(x2)
由单调性定义知f(x)为[1,+∞)单调增函数.(8分)
(2)当a=
时,同理可证f(x)在[1,∞)是增函数,(10分)
∴当x=1时,f(x)的最小值为f(1)=
(12分)
又f(x)无最大值,(14分)
∴f(x)只存在最小值为
.(15分)
(若用导数处理则类似给分)
证明:任取x1,x2∈[1,+∞)且x1<x2,则
f(x1)-f(x2)=
| x12+2x1+a |
| x1 |
| x22+2x2+a |
| x2 |
| (x1-x2)(x1x2-a) |
| x1x2 |
∵x1,x2∈[1,+∞)且x1<x2,a<0
∴
| (x1-x2)(x1x2-a) |
| x1x2 |
∴f(x1)<f(x2)
由单调性定义知f(x)为[1,+∞)单调增函数.(8分)
(2)当a=
| 1 |
| 2 |
∴当x=1时,f(x)的最小值为f(1)=
| 7 |
| 2 |
又f(x)无最大值,(14分)
∴f(x)只存在最小值为
| 7 |
| 2 |
(若用导数处理则类似给分)

练习册系列答案
相关题目
已知奇函数f(x)在[-1,0]上为单调减函数,又α,β为锐角三角形内角,则( )
| A、f(cosα)>f(cosβ) | B、f(sinα)>f(sinβ) | C、f(sinα)<f(cosβ) | D、f(sinα)>f(cosβ) |
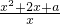 ,x∈[1,∞).
,x∈[1,∞). 时,求函数f(x)的最值.
时,求函数f(x)的最值.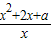 ,x∈[1,∞).
,x∈[1,∞). 时,求函数f(x)的最值.
时,求函数f(x)的最值.