题目内容
4.从8名教师中选派4人去参加一个研讨会,其中教师甲是领队必须去,而乙、丙两位教师不能同去,则不同的选派方法有30种.分析 题目对于元素有限制,注意先安排有限制条件的元素,乙、丙两位教师不能同去,可以分情况讨论,乙、丙两位教师去其中一位,;乙、丙都不去,根据分类计数原理得到结果.
解答 解:从8名教师中选派4人去参加一个研讨会,其中教师甲是领队必须去,而乙、丙两位教师不能同去,可以分情况讨论,
①乙、丙两位教师去其中一位,有C21•C52=20种选法;
②乙、丙都不去,有C53=10种选法,
共有20+10=30种不同的选派方法,
故答案为:30.
点评 本题考查了分类加法计数原理,首先确定分类标准,其次满足完成这件事的任何一种方法必属某一类,并且分别属于不同的两类的方法都是不同的方法,即做到不重不漏.

练习册系列答案
相关题目
12.直三棱柱ABC-A1B1C1中,∠B1BC1=30°,AB=BC=CA,M、N分别是棱AA1、A1B1中点,则MN与AC所成的角的余弦值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{1}{3}$ |
16.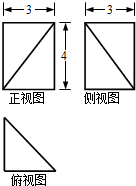 若某几何体的三视图(单位:cm)如图所示,则该几何体的体积为( )
若某几何体的三视图(单位:cm)如图所示,则该几何体的体积为( )
 若某几何体的三视图(单位:cm)如图所示,则该几何体的体积为( )
若某几何体的三视图(单位:cm)如图所示,则该几何体的体积为( )| A. | 6cm3 | B. | 12cm3 | C. | 18cm3 | D. | 36cm3 |
 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$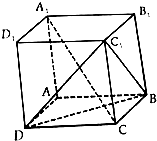 如图所示,已知棱长为1的正方体ABCD-A1B1C1D1
如图所示,已知棱长为1的正方体ABCD-A1B1C1D1