题目内容
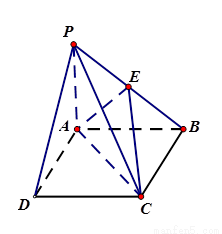
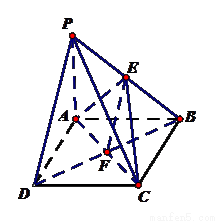
(13分)如图,在四棱锥 中,底面
中,底面 为边长为4的正方形,
为边长为4的正方形, 平面
平面 ,
, 为
为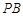 中点,
中点, 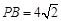 .
.
(1)求证: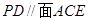 .
.
(2)求三棱锥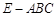 的体积.
的体积.
【答案】
(1)证明:连接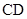 ,交AB于F,连接EF.
,交AB于F,连接EF.
推出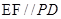 进一步得到
进一步得到 .
.
(2)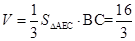 .
.
【解析】
试题分析:(1)证明:因为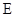 为
为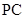 的中点,连接
的中点,连接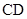 ,交AB于F,连接EF.
,交AB于F,连接EF.

 四边形
四边形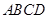 为正方形
为正方形  为CD的中点
为CD的中点
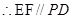
又 PD?面 ABE,EF?面ABE,
PD?面 ABE,EF?面ABE,
 . …………………………………5分
. …………………………………5分
(2) 四边形
四边形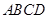 为正方形
为正方形 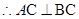
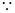
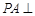 平面
平面 ,
,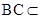 平面
平面
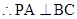
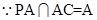
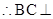 面PAC
面PAC
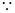
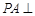 平面
平面 ,
,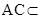 平面
平面
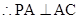
…………………………………10分
在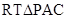 中,
中, ,AC=4,则
,AC=4,则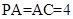
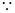
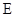 为
为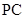 的中点
的中点 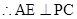
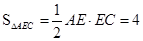
 …………………………………13分
…………………………………13分
考点:本题主要考查立体几何中平行、垂直及几何体体积的计算。
点评:典型题,立体几何中平行、垂直关系的证明及角的计算问题是高考中的必考题,象立体几何中的计算问题,往往要“一作、二证、三计算”。

练习册系列答案
相关题目
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.
 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小. 中,底面
中,底面 是菱形,
是菱形, ,
, ,
, ,
, 平面
平面 是
是 的中点,
的中点, 是
是 的中点.
的中点.  ∥平面
∥平面 ;
; ;
; 所成的锐二面角的大小.
所成的锐二面角的大小.
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
. 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小.
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ,
, 为
为 中点,作
中点,作 交
交 于
于

 与平面
与平面 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。 中,底面
中,底面 为平行四边形,
为平行四边形, 平面
平面

 在棱
在棱 上.
上.
 时,求证
时,求证 平面
平面
 的大小为
的大小为 时,求直线
时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.