Question

已知A(3，

3

)，O为原点，点P（x，y）的坐标满足

3 x-y≤0 x- 3 y+2≥0 y≥0

，则

OA • OP

| OA |

的最大值是

 

，此时点P的坐标是

 

．

Answer 1

分析：观察题设条件，需要先求出向量

OA

，

OP

的坐标，将

OA • OP

| OA |

转化，再作出不等式组

3 x-y≤0 x- 3 y+2≥0 y≥0

对应的区域，由图形判断出最大值点P的坐标即可．

解答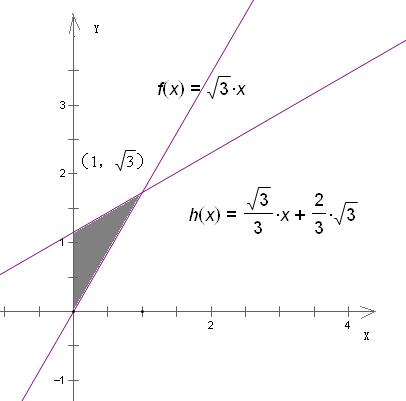：解：由题意向量

OA

，

OP

的坐标分别为(3，

3

)，（x，y）
故

OA • OP

| OA |

=

3x+ 3 y

2 3

=

3

2

x+

y

2

不等式组

3 x-y≤0 x- 3 y+2≥0 y≥0

对应的区域，如图
由图知

OA • OP

| OA |

=

3

2

x+

y

2

在点（1，

3

）取到最大值

3

故P（1，

3

）
故答案为：

3

，（1，

3

）

点评：本题考查简单线性规划，求解此类问题的关键是正确作图，熟练掌握目标函数最值的判断方法，判断目标函数的最值是本部分中的难点，也是易错点．