题目内容
已知四棱锥 的底面为直角梯形,
的底面为直角梯形, ,
, 底面
底面 ,且
,且 ,
, ,
, 是
是 的中点。
的中点。

(Ⅰ)证明:面 面
面 ;
;
(Ⅱ)求 与
与 所成的角;
所成的角;
(Ⅲ)求面 与面
与面 所成二面角的大小。
所成二面角的大小。
 的底面为直角梯形,
的底面为直角梯形, ,
, 底面
底面 ,且
,且 ,
, ,
, 是
是 的中点。
的中点。
(Ⅰ)证明:面
 面
面 ;
;(Ⅱ)求
 与
与 所成的角;
所成的角;(Ⅲ)求面
 与面
与面 所成二面角的大小。
所成二面角的大小。(1)由题设知 ,且
,且 与
与 是平面
是平面 内的两条相交直线,由此得
内的两条相交直线,由此得 面
面 .又
.又 在面
在面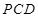 上,故面
上,故面 ⊥面
⊥面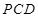
(2)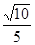
(3)
 ,且
,且 与
与 是平面
是平面 内的两条相交直线,由此得
内的两条相交直线,由此得 面
面 .又
.又 在面
在面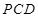 上,故面
上,故面 ⊥面
⊥面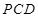
(2)
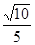
(3)

试题分析:证明:以
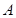 为坐标原点
为坐标原点 长为单位长度,如图建立空间直角坐标系,则各点坐标为
长为单位长度,如图建立空间直角坐标系,则各点坐标为 .
.(Ⅰ)证明:因

由题设知
 ,且
,且 与
与 是平面
是平面 内的两条相交直线,由此得
内的两条相交直线,由此得 面
面 .又
.又 在面
在面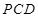 上,故面
上,故面 ⊥面
⊥面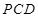 .
.
(Ⅱ)解:因


(Ⅲ)解:在
 上取一点
上取一点 ,则存在
,则存在 使
使

要使


 为
为所求二面角的平面角.

点评:主要是考查了线面角以及二面角的求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
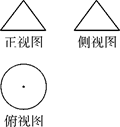




 的半圆,俯视图是半径为
的半圆,俯视图是半径为 ,则
,则 ______.
______.

 中,
中, 分别是棱
分别是棱 的中点,则
的中点,则 与平面BB1D1D的位置关系是( )
与平面BB1D1D的位置关系是( )
 平面
平面
 的矩形.则该几何体的表面积是( )
的矩形.则该几何体的表面积是( )












 的顶点都在半径为3的球的球面上,那么该长方体表面积的最大值等于_____________;
的顶点都在半径为3的球的球面上,那么该长方体表面积的最大值等于_____________;