题目内容
设椭圆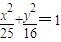 上一点P到左准线的距离为10,F是该椭圆的左焦点,若点M满足
上一点P到左准线的距离为10,F是该椭圆的左焦点,若点M满足 =
= (
( +
+ ),则
),则 = .
= .
【答案】分析:根据a2-b2=c2求出左焦点F的坐标,根据椭圆的准线公式x=-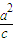 求出左准线方程,然后设P的坐标(x,y),根据两点间的距离公式求出P到准线方程的距离让其等于10求出x,然后再把x的值代入到椭圆方程中得到P的坐标,由
求出左准线方程,然后设P的坐标(x,y),根据两点间的距离公式求出P到准线方程的距离让其等于10求出x,然后再把x的值代入到椭圆方程中得到P的坐标,由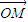 =
= (
(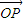 +
+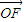 )得到M为PF的中点,根据中点坐标公式求出M的坐标,利用两点间的距离公式求出
)得到M为PF的中点,根据中点坐标公式求出M的坐标,利用两点间的距离公式求出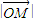 即可.
即可.
解答:解:由椭圆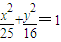 得a=5,b=4,
得a=5,b=4,
根据勾股定理得c=3,则左准线为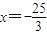 ,左焦点F(-3,0),
,左焦点F(-3,0),
设P(x,y),因为P到左准线的距离为10,列出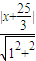 =10,
=10,
解得x= 或x=-
或x=-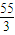 (舍去);
(舍去);
又P在椭圆上,则将x= 代入到椭圆方程中求出y=
代入到椭圆方程中求出y=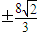 ,
,
所以点P( ,
,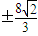 );
);
由点M满足 =
= (
(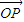 +
+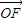 ),则得M为PF中点,
),则得M为PF中点,
根据中点坐标公式求得M(- ,±
,±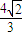 ),
),
所以 =
=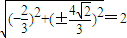
故答案为2.
点评:本题是一道综合题,考查学生掌握椭圆的一些简单性质,会利用两点间的距离公式及中点坐标公式、点到直线的距离公式化简求值,同时也考查学生掌握向量的运用法则及向量模的求法,做题时要求学生知识面要宽,综合运用数学知识解决问题.
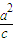 求出左准线方程,然后设P的坐标(x,y),根据两点间的距离公式求出P到准线方程的距离让其等于10求出x,然后再把x的值代入到椭圆方程中得到P的坐标,由
求出左准线方程,然后设P的坐标(x,y),根据两点间的距离公式求出P到准线方程的距离让其等于10求出x,然后再把x的值代入到椭圆方程中得到P的坐标,由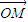 =
= (
(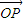 +
+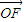 )得到M为PF的中点,根据中点坐标公式求出M的坐标,利用两点间的距离公式求出
)得到M为PF的中点,根据中点坐标公式求出M的坐标,利用两点间的距离公式求出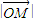 即可.
即可.解答:解:由椭圆
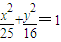 得a=5,b=4,
得a=5,b=4,根据勾股定理得c=3,则左准线为
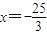 ,左焦点F(-3,0),
,左焦点F(-3,0),设P(x,y),因为P到左准线的距离为10,列出
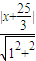 =10,
=10,解得x=
 或x=-
或x=-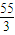 (舍去);
(舍去);又P在椭圆上,则将x=
 代入到椭圆方程中求出y=
代入到椭圆方程中求出y=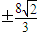 ,
,所以点P(
 ,
,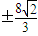 );
);由点M满足
 =
= (
(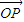 +
+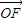 ),则得M为PF中点,
),则得M为PF中点,根据中点坐标公式求得M(-
 ,±
,±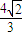 ),
),所以
 =
=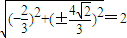
故答案为2.
点评:本题是一道综合题,考查学生掌握椭圆的一些简单性质,会利用两点间的距离公式及中点坐标公式、点到直线的距离公式化简求值,同时也考查学生掌握向量的运用法则及向量模的求法,做题时要求学生知识面要宽,综合运用数学知识解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
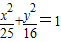 上一点P到左准线的距离为10,F是该椭圆的左焦点,若点M满足
上一点P到左准线的距离为10,F是该椭圆的左焦点,若点M满足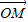 =
= (
(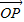 +
+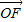 ),则
),则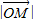 = .
= .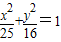 上一点P到左准线的距离为10,F是该椭圆的左焦点,若点M满足
上一点P到左准线的距离为10,F是该椭圆的左焦点,若点M满足 =
= (
( +
+ ),则
),则 = .
= . 上一点P到左准线的距离为10,F是该椭圆的左焦点,若点M满足
上一点P到左准线的距离为10,F是该椭圆的左焦点,若点M满足 =
= (
( +
+ ),则
),则 = .
= . 上一点P到左准线的距离为10,F是该椭圆的左焦点,若点M满足
上一点P到左准线的距离为10,F是该椭圆的左焦点,若点M满足 =
= (
( +
+ ),则
),则 = .
= .