题目内容
已知钝角三角形ABC的最大边长是2,其余两边长分别是a,b,则集合P={(x,y)|x=a,y=b}所表示的平面图形的面积是
π-2
π-2
.分析:由三角形的边长大于0,两边之和大于第三边,及最大边所对的角是钝角列出约束条件,画出图形后找到可行域,由四分之一圆的面积减去三角形面积得答案.
解答:解:由题意:a+b>2,
cosC=
<0,
a>0,b>0
∴集合P={(x,y)|x=a,y=b}对应的约束条件为
画出平面区域可得如图,
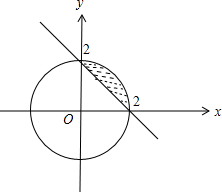
∴S=
×4π-
×2×2=π-2.
故答案为π-2.
cosC=
| a2+b2-4 |
| 2ab |
a>0,b>0
∴集合P={(x,y)|x=a,y=b}对应的约束条件为
|
画出平面区域可得如图,

∴S=
| 1 |
| 4 |
| 1 |
| 2 |
故答案为π-2.
点评:本题考查了余弦定理,考查了三角形的边角关系,考查了数形结合的解题思想,是简单的线性规划题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目