题目内容
设a为大于0的常数,函数f(x)=| x |
(1)当a=
| 3 |
| 4 |
(2)若使函数f(x)为增函数,求a的取值范围.
分析:(1)将a的值代入后对函数进行求导,令导函数等于0求出x的值,然后判断函数的单调性进而可求极大值与极小值.
(2)将问题转化为函数f(x)的导函数在∈[0,+∞)大于等于0恒成立的问题,从而得解.
(2)将问题转化为函数f(x)的导函数在∈[0,+∞)大于等于0恒成立的问题,从而得解.
解答:解:(1)当a=
时,f′(x)=
-
,
令f′(x)=0,则x-2
+
=0,∴x=
或
,
当x∈[0,
]时,f′(x)>0,当x∈(
,
),f′(x)<0,
当x∈(
,+∞)时,f′(x)>0,
∴f(x)极大值=f(
)=
,f(x)极小值=f(
)=
-ln3.
(2)f′(x)=
-
,若f(x)为增函数,则当x∈[0,+∞)时,f′(x)≥0恒成立,
∴
≥
,即x+a≥2
,
即a≥2
-x=-(
-1)2+1恒成立,
∴a≥1.
| 3 |
| 4 |
| 1 | ||
2
|
| 1 | ||
x+
|
令f′(x)=0,则x-2
| x |
| 3 |
| 4 |
| 9 |
| 4 |
| 1 |
| 4 |
当x∈[0,
| 1 |
| 4 |
| 1 |
| 4 |
| 9 |
| 4 |
当x∈(
| 9 |
| 4 |
∴f(x)极大值=f(
| 1 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
(2)f′(x)=
| 1 | ||
2
|
| 1 |
| x+a |
∴
| 1 | ||
2
|
| 1 |
| x+a |
| x |
即a≥2
| x |
| x |
∴a≥1.
点评:本题主要考查函数的单调性、极值点与其导函数之间的关系.导数问题时每年高考的热点,要重视.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
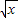 -ln(x+a).
-ln(x+a). ,求函数f(x)的极大值和极小值;
,求函数f(x)的极大值和极小值;