题目内容
设Sn是各项均为非零实数的数列{an}的前n项和,给出如下两个命题上:命题p:{an}是等差数列;命题q:等式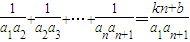 对任意n(n∈N*)恒成立,其中k,b是常数.
对任意n(n∈N*)恒成立,其中k,b是常数.(1)若p是q的充分条件,求k,b的值;
(2)对于(1)中的k与b,问p是否为q的必要条件,请说明理由;
(3)若p为真命题,对于给定的正整数n(n>1)和正数M,数列{an}满足条件
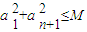 ,试求Sn的最大值.
,试求Sn的最大值.
【答案】分析:(1)设{an}的公差为d,利用裂项法原等式可化为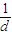 (
(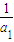 -
-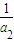 +
+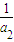 -
-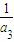 +…+
+…+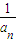 -
-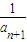 )=
)=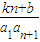 ,整理可得(k-1)n+b=0对于n∈N*恒成立,从而可求得k,b的值;
,整理可得(k-1)n+b=0对于n∈N*恒成立,从而可求得k,b的值;
(2)当k=1,b=0时,假设p是q的必要条件,分当n=1时,当n≥2时,当n≥3时讨论即可判断结论是否正确;
(3)由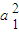 +
+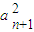 ≤M,可设a1=rcosθ,an+1=rsinθ,代入求和公式Sn=
≤M,可设a1=rcosθ,an+1=rsinθ,代入求和公式Sn=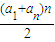 ,利用三角函数的有界性即可求得其最大值.
,利用三角函数的有界性即可求得其最大值.
解答:解:(1)设{an}的公差为d,则原等式可化为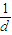 (
(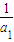 -
- +
+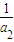 -
-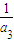 +…+
+…+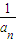 -
-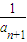 )=
)=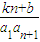 ,
,
所以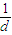 •
•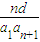 =
=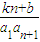 ,
,
即(k-1)n+b=0对于n∈N*恒成立,所以k=1,b=0.…(4分)
(2)当k=1,b=0时,假设p是q的必要条件,即“若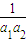 +
+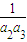 +…+
+…+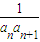 =
=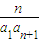 ①对于任意的n(n∈N*)恒成立,则{an}为等差数列”.
①对于任意的n(n∈N*)恒成立,则{an}为等差数列”.
当n=1时,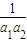 =
=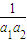 显然成立.…(6分)
显然成立.…(6分)
当n≥2时,若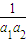 +
+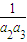 +…+
+…+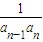 =
=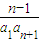 ②,
②,
由①-②得,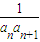 =
=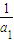 (
( -
-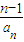 ),即nan-(n-1)an+1=a1③.
),即nan-(n-1)an+1=a1③.
当n=2时,a1+a3=2a2,即a1、a2、a3成等差数列,
当n≥3时,(n-1)an-1-(n-2)an=a1④,即2an=an-1+an+1.所以{an}为等差数列,即p是q的必要条件.…(10分)
(3)由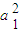 +
+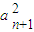 ≤M,可设a1=rcosθ,an+1=rsinθ,所以r≤
≤M,可设a1=rcosθ,an+1=rsinθ,所以r≤ .
.
设{an}的公差为d,则an+1-a1=nd=rsinθ-rcosθ,
所以d=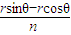 ,
,
所以an=rsinθ-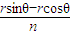 ,
,
Sn=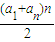 =
=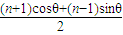 r≤
r≤ •
•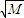 =
=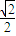
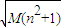 ,
,
所以Sn的最大值为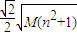 …(16分)
…(16分)
点评:本题考查等差数列与等比数列的综合,突出考查“充分、必要条件”在数列中的综合应用,判断(2)中“p是否为q的必要条件”是难点,考查参数方程及三角函数的有界性,属于难题.
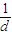 (
(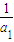 -
-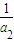 +
+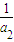 -
-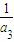 +…+
+…+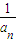 -
-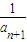 )=
)=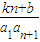 ,整理可得(k-1)n+b=0对于n∈N*恒成立,从而可求得k,b的值;
,整理可得(k-1)n+b=0对于n∈N*恒成立,从而可求得k,b的值;(2)当k=1,b=0时,假设p是q的必要条件,分当n=1时,当n≥2时,当n≥3时讨论即可判断结论是否正确;
(3)由
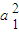 +
+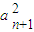 ≤M,可设a1=rcosθ,an+1=rsinθ,代入求和公式Sn=
≤M,可设a1=rcosθ,an+1=rsinθ,代入求和公式Sn=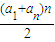 ,利用三角函数的有界性即可求得其最大值.
,利用三角函数的有界性即可求得其最大值.解答:解:(1)设{an}的公差为d,则原等式可化为
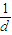 (
(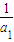 -
- +
+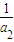 -
-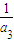 +…+
+…+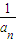 -
-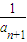 )=
)=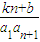 ,
,所以
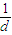 •
•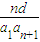 =
=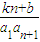 ,
,即(k-1)n+b=0对于n∈N*恒成立,所以k=1,b=0.…(4分)
(2)当k=1,b=0时,假设p是q的必要条件,即“若
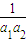 +
+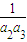 +…+
+…+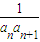 =
=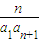 ①对于任意的n(n∈N*)恒成立,则{an}为等差数列”.
①对于任意的n(n∈N*)恒成立,则{an}为等差数列”.当n=1时,
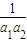 =
=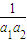 显然成立.…(6分)
显然成立.…(6分)当n≥2时,若
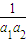 +
+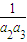 +…+
+…+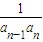 =
=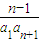 ②,
②,由①-②得,
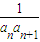 =
=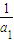 (
( -
-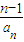 ),即nan-(n-1)an+1=a1③.
),即nan-(n-1)an+1=a1③.当n=2时,a1+a3=2a2,即a1、a2、a3成等差数列,
当n≥3时,(n-1)an-1-(n-2)an=a1④,即2an=an-1+an+1.所以{an}为等差数列,即p是q的必要条件.…(10分)
(3)由
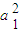 +
+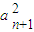 ≤M,可设a1=rcosθ,an+1=rsinθ,所以r≤
≤M,可设a1=rcosθ,an+1=rsinθ,所以r≤ .
.设{an}的公差为d,则an+1-a1=nd=rsinθ-rcosθ,
所以d=
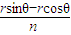 ,
,所以an=rsinθ-
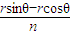 ,
,Sn=
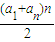 =
=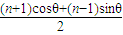 r≤
r≤ •
•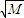 =
=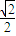
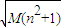 ,
,所以Sn的最大值为
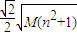 …(16分)
…(16分)点评:本题考查等差数列与等比数列的综合,突出考查“充分、必要条件”在数列中的综合应用,判断(2)中“p是否为q的必要条件”是难点,考查参数方程及三角函数的有界性,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目