题目内容
(本小题满分13分)
已知函数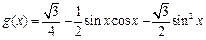 的图象按向量
的图象按向量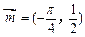 平移得到函数
平移得到函数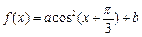 的图象.
的图象.
(1) 求实数a、b的值;
(2) 设函数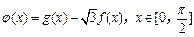 ,求函数
,求函数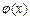 的单调递增区间和最值.
的单调递增区间和最值.
已知函数
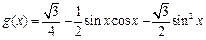 的图象按向量
的图象按向量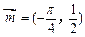 平移得到函数
平移得到函数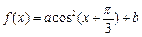 的图象.
的图象.(1) 求实数a、b的值;
(2) 设函数
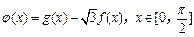 ,求函数
,求函数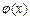 的单调递增区间和最值.
的单调递增区间和最值.(1)a=1,b=0(2)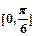 ,
,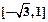
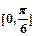 ,
,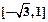
(1) 依题意按向量0平移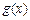 得
得
f(x)-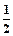 =
=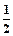 sin[2(x+
sin[2(x+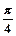 )+
)+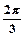 ] 得f(x)=-
] 得f(x)=-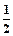 sin(2x+
sin(2x+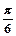 )+
)+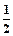
又f(x)=acos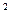 (x+
(x+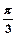 )+b=-
)+b=-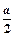 sin(2x+
sin(2x+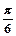 )+
)+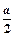 +b
+b
比较得a=1,b=0 ··································································· 6分
(2)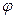 (x)=g(x)-
(x)=g(x)-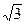 f(x)=
f(x)=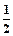 sin(2x+
sin(2x+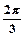 )-
)-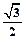 cos(2x+
cos(2x+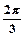 )-
)-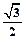 =sin(2x+
=sin(2x+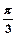 )-
)-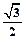
∴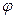 (x)的单调增区间为
(x)的单调增区间为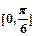 ,值域为
,值域为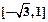 13分
13分
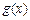 得
得f(x)-
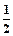 =
=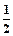 sin[2(x+
sin[2(x+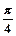 )+
)+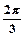 ] 得f(x)=-
] 得f(x)=-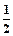 sin(2x+
sin(2x+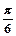 )+
)+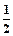
又f(x)=acos
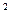 (x+
(x+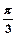 )+b=-
)+b=-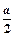 sin(2x+
sin(2x+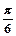 )+
)+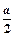 +b
+b 比较得a=1,b=0 ··································································· 6分
(2)
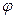 (x)=g(x)-
(x)=g(x)-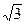 f(x)=
f(x)=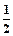 sin(2x+
sin(2x+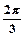 )-
)-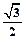 cos(2x+
cos(2x+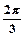 )-
)-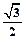 =sin(2x+
=sin(2x+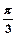 )-
)-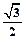
∴
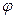 (x)的单调增区间为
(x)的单调增区间为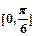 ,值域为
,值域为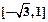 13分
13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
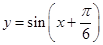
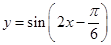
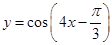

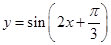
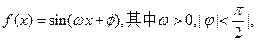
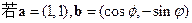 ,且
,且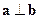 ,又知函数
,又知函数 (1)求
(1)求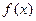 的解析式;
的解析式;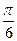 个单位得到
个单位得到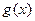 的图象,求
的图象,求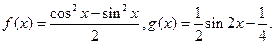
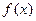 的图象可由函数
的图象可由函数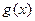 的图象经过怎样变化得出?
的图象经过怎样变化得出?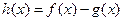 的最小值,并求使用
的最小值,并求使用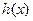 取得最小值的
取得最小值的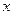 的集合。
的集合。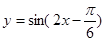 的图象,可以将函数
的图象,可以将函数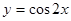 的图象( )
的图象( )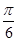 个单位长度
个单位长度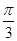 个单位长度
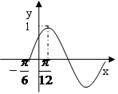
个单位长度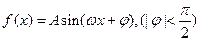 的部分图象如右图示,
的部分图象如右图示,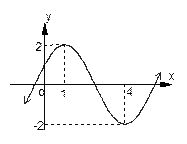
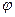 分别为
分别为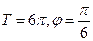
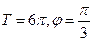
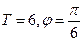
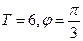
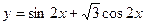 的图象按向量a平移后所得的图象关于x轴对称,那么向量a可以是 ( )
的图象按向量a平移后所得的图象关于x轴对称,那么向量a可以是 ( )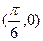
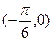
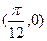
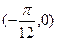
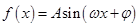
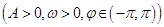 图像的一部分,则
图像的一部分,则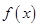 的解析式为 .
的解析式为 .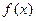 的定义域为R,最小正周期为
的定义域为R,最小正周期为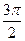 的函数,若
的函数,若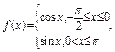
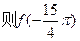 =_____________________。
=_____________________。