题目内容
已知函数y=Asin(ωx+φ)(A>0,ω>0)在同一周期内,当x=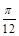 时,ymax=2;当
时,ymax=2;当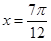 时,ymin=-2.那么函数的解析式为 ( )
时,ymin=-2.那么函数的解析式为 ( )
A.y=2sin(2x+ ) ) | B.y=2sin(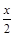 - -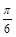 ) ) |
C.y=2sin(2x+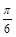 ) ) | D.y=2sin(2x- ) ) |
A
解析试题分析:由题意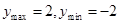 可得A=2,
可得A=2, ,∴
,∴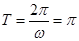 ,∴
,∴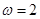 ,排除B
,排除B
又∵当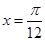 时,
时,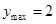 ,∴
,∴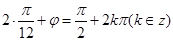 ,∴
,∴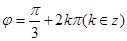 ,A,C,D中只有A符合,故选A.
,A,C,D中只有A符合,故选A.
考点:三角函数的图像与性质.

练习册系列答案
相关题目
函数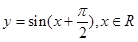 是( )
是( )
A.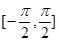 上是增函数 上是增函数 | B.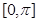 上是减函数 上是减函数 |
C.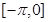 上是减函数 上是减函数 | D.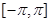 上是减函数 上是减函数 |
函数 的最小正周期是( )
的最小正周期是( )
A. | B. | C. | D. |
已知角θ的终边上有一点 P(-4,3) , 则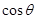 的值是 ( )
的值是 ( )
A. | B.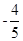 | C.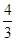 | D.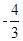 |
已知
 ,满足
,满足 ,
, ,则
,则 在区间
在区间 上的最大值与最小值之和为( )
上的最大值与最小值之和为( )
A. | B. | C. | D. |
已知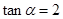 ,则
,则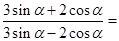 ( )
( )
| A.2 | B.1 | C.4 | D.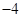 |
在 内,使
内,使 成立的
成立的 取值范围为( )
取值范围为( )
A. | B.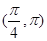 | C. | D. |
[2014·海淀模拟]同时具有下列性质:“①对任意x∈R,f(x+π)=f(x)恒成立;②图象关于直线x= 对称;③在[-
对称;③在[- ,
, ]上是增函数”的函数可以是( )
]上是增函数”的函数可以是( )
A.f(x)=sin(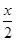 + + ) ) | B.f(x)=sin(2x- ) ) |
C.f(x)=cos(2x+ ) ) | D.f(x)=cos(2x- ) ) |
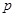 :函数
:函数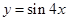 是最小正周期为
是最小正周期为 的周期函数,命题
的周期函数,命题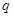 :函数
:函数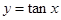 在
在 上单调递减,则下列命题为真命题的是( )
上单调递减,则下列命题为真命题的是( )