题目内容
已知两条直线 与
与 的交点
的交点 ,求:(1)过点
,求:(1)过点 且过原点的直线方程;(2)过点
且过原点的直线方程;(2)过点 且垂直于直线
且垂直于直线 的直线
的直线 的方程。
的方程。
【答案】
(1)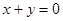 (2)
(2)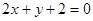
【解析】
试题分析:解:(1)由题意直线l1:3x+4y-2=0与直线l2:2x+y+2=0联立: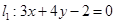 与
与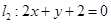 ,解得x=-2,y=2则交点P(-2,2)所以,过点P(-2,2)与原点的直线方程为:,化简得:x+y=0;(2)直线l3:x-2y-1=0的斜率为k=
,解得x=-2,y=2则交点P(-2,2)所以,过点P(-2,2)与原点的直线方程为:,化简得:x+y=0;(2)直线l3:x-2y-1=0的斜率为k=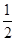 过点P(-2,2)且垂直于直线l3:x-2y-1=0的直线l的斜率为-2.所以,由点斜式所求直线的方程y-2=-2(x+2)即所求直线的方程2x+y+2=0
过点P(-2,2)且垂直于直线l3:x-2y-1=0的直线l的斜率为-2.所以,由点斜式所求直线的方程y-2=-2(x+2)即所求直线的方程2x+y+2=0
考点:两直线的交点坐标,两直线的垂直关系
点评:此题是一道中档题,要求学生会求两直线的交点坐标,掌握两直线垂直时斜率之间的关系,会根据条件写出直线的点斜式方程和两点式方程

练习册系列答案
相关题目
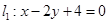 与
与 的交点为P,直
的交点为P,直 的方程为:
的方程为: .
. 与
与 的交点P,
的交点P, 的直线
的直线 的方程;
的方程; 与直线
与直线 垂直,求
垂直,求 .
.