题目内容
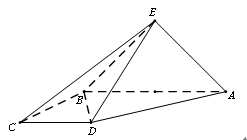
如图,平面ABCD⊥平面ABEF,又ABCD是正方形,ABEF是矩形,且 G是EF的中
G是EF的中
点.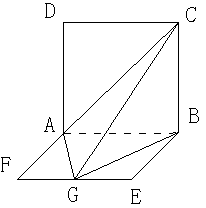
(1)求证:平面AGC⊥平面BGC;
(2)求GB与平面AGC所成角的正弦值.
(1)先证AG⊥平面CBG (2)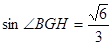
解析试题分析:(1)证.正方形ABCD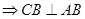 ,∵面ABCD⊥面ABEF且交于AB,∴CB⊥面ABEF
,∵面ABCD⊥面ABEF且交于AB,∴CB⊥面ABEF
∵AG,GB 面ABEF, ∴CB⊥AG,CB⊥BG.又AD=2a,AF= a, ABEF是矩形,G是EF的中点.
面ABEF, ∴CB⊥AG,CB⊥BG.又AD=2a,AF= a, ABEF是矩形,G是EF的中点.
∴AG=BG=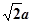 ,AB=2a, AB2=AG2+BG2, ∴AG⊥BG,∵BC∩BG=B,∴AG⊥平面CBG,而AG
,AB=2a, AB2=AG2+BG2, ∴AG⊥BG,∵BC∩BG=B,∴AG⊥平面CBG,而AG 面AGC,故平
面AGC,故平
面AGC⊥平面BGC.
(2)解.如图,由(1)知面AGC⊥面BGC,且交于GC,在平面BGC内作BH⊥GC,垂足为H,则BH⊥平面AGC,
∴∠BGH是GB与平面AGC所成的角.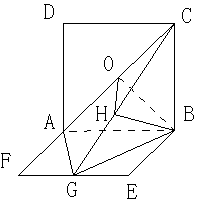
∴在R t△CBG中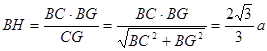
又BG=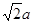 ,∴
,∴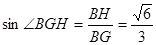
考点:平面与平面垂直的判定;直线与平面所成的角.
点评:本题考查面面垂直的判定方法,以及求线面成的角的求法,体现转化的思想.

练习册系列答案
相关题目
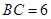 ,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.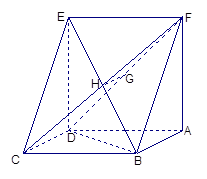
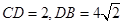 ,求四棱锥F-ABCD的体积.
,求四棱锥F-ABCD的体积.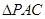 与
与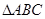 是均以
是均以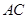 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, ,
,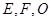 分别为
分别为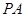 ,
,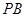 ,
,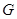 为
为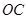 的中点,且
的中点,且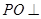 平面
平面 .
.
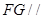 平面
平面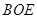 ;
;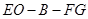 的余弦值.
的余弦值.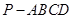 中,
中,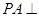 底面
底面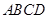 ,
,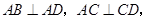
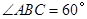 ,
,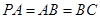 ,
,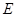 是
是 的中点.
的中点.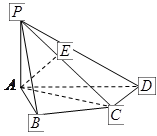
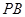 和平面
和平面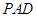 所成的角的大小;
所成的角的大小;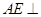 平面
平面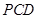 ;
;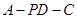 的正弦值.
的正弦值. ,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。
,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。
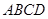 与等腰直角三角形
与等腰直角三角形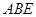 所在的平面互相垂直.
所在的平面互相垂直.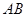 ∥
∥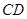 ,
,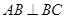 ,
, ,
, .
.
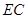 与平面
与平面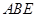 所成角的正弦值;
所成角的正弦值;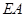 上是否存在点
上是否存在点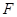 ,使
,使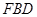 ?若存在,求出
?若存在,求出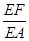 ;若不存在,说明理由.1
;若不存在,说明理由.1
 平面EFGH;
平面EFGH; 中,对角线
中,对角线 于
于 ,
, ,
,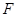 为
为 的重心,过点
的重心,过点 分别交
分别交 于
于 且
且 ,沿
,沿 将
将 折起,沿
折起,沿 折起,
折起, 正好重合于
正好重合于 .
. 
 平面
平面 ;
;  与平面
与平面 夹角的大小.
夹角的大小. 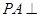 ⊙
⊙ 所在的平面,AB是⊙
所在的平面,AB是⊙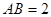 ,
, 是⊙
是⊙ ,
,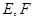 分别为
分别为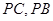 中点。
中点。
 平面
平面 ;
;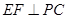 ;
; -
-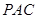 的体积。
的体积。