题目内容
“-4<k<0”是“曲线y=kx2-kx-1恒在x轴下方”的_______条件.
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既非充分又非必要
A
分析:通过对x2的项的系数的分类讨论,利用二次函数的图象与性质即可得出.
解答:①k=0时,曲线y=-1恒在x轴下方;
②k≠0时,要使曲线y=kx2-kx-1恒在x轴下方,则必须满足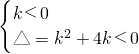 ,解得-4<k<0.
,解得-4<k<0.
综上①②可知:曲线y=kx2-kx-1恒在x轴下方的充要条件是-4<k≤0.
因此“-4<k<0”是“曲线y=kx2-kx-1恒在x轴下方”的充分不必要条件.
故选A.
点评:熟练掌握二次函数的图象与性质是解题的关键.注意分类讨论的思想方法的应用.
分析:通过对x2的项的系数的分类讨论,利用二次函数的图象与性质即可得出.
解答:①k=0时,曲线y=-1恒在x轴下方;
②k≠0时,要使曲线y=kx2-kx-1恒在x轴下方,则必须满足
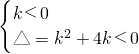 ,解得-4<k<0.
,解得-4<k<0.综上①②可知:曲线y=kx2-kx-1恒在x轴下方的充要条件是-4<k≤0.
因此“-4<k<0”是“曲线y=kx2-kx-1恒在x轴下方”的充分不必要条件.
故选A.
点评:熟练掌握二次函数的图象与性质是解题的关键.注意分类讨论的思想方法的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目