题目内容
已知全集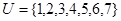 ,集合
,集合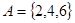 ,集合
,集合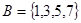 ,则
,则 等于( )
等于( )
A. | B. | C.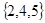 | D.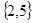 |
A
解析试题分析:根据题意可知,全集中共有7个连续的自然数元素,而要求解交集和补集,则根据补集的概念求解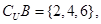 ,再根据交集的含义可知,
,再根据交集的含义可知,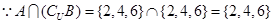 ,故答案为A.
,故答案为A.
考点:本题主要考查集合的交集和补集的运算问题,属于基础题型。
点评:解决对于给定的有限集合补集的运算,准确理解全集,结合概念求解补集,同时对于交集和补集的复合运算,一般可以分为两步来完成。

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
已知集合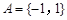 ,
,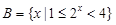 ,则
,则 等于( )
等于( )
A.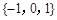 | B.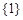 | C.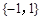 | D.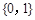 |
设集合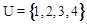 ,
,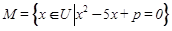 ,若
,若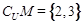 ,则实数
,则实数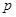 的值为
的值为
A.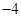 | B.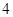 | C.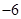 | D.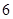 |
 表示自然数集,集合
表示自然数集,集合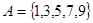
 ,则
,则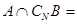 ( )
( )
A.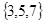 | B.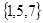 | C. | D. |
若集合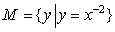 ,
, ,那么
,那么 ( )
( )
A. | B. | C. | D.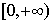 |
已知M,N为集合I的非空真子集,且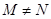 ,若
,若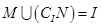 ,则
,则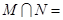 ( )
( )
| A.M | B.N | C.I | D.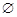 |
设集合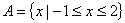 ,
,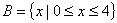 ,则
,则 ( )
( )
A. | B.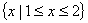 |
C. | D. |
设集合A={2,3},B={3,4},C={3,4,5}则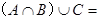 ( )
( )
| A.{2,3,4} | B.{2,3,5} | C.{3,4,5} | D.{2,3,4,5} |
如果集合M={y|y= },则M的真子集个数为( )
},则M的真子集个数为( )
| A.3 | B.7 | C.15 | D.无穷多个 |