题目内容
设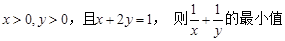 .
.
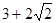
解析试题分析:因为,
所以,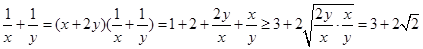 ,
,
故答案为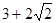 。
。
考点:均值定理的应用
点评:简单题,应用均值定理,要注意“一正,二定,三相等”,缺一不可。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
题目内容
设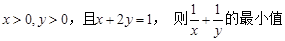 .
.
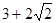
解析试题分析:因为,
所以,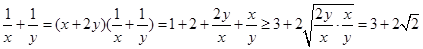 ,
,
故答案为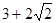 。
。
考点:均值定理的应用
点评:简单题,应用均值定理,要注意“一正,二定,三相等”,缺一不可。

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案