题目内容
(1)已知扇形的周长为10,面积为4,求扇形中心角的弧度数;
(2)已知扇形的周长为40,当它的半径和中心角取何值时,才能使扇形的面积最大?最大面积是多少?
(2)已知扇形的周长为40,当它的半径和中心角取何值时,才能使扇形的面积最大?最大面积是多少?
(1) =
= (2)R="10,"
(2)R="10,"  =2时面积取得最大值,最大值为100
=2时面积取得最大值,最大值为100
 =
= (2)R="10,"
(2)R="10,"  =2时面积取得最大值,最大值为100
=2时面积取得最大值,最大值为100设扇形半径为R,中心角为 ,所对的弧长为l.
,所对的弧长为l.
(1)依题意,得
∴2 2-17
2-17 +8=0,∴
+8=0,∴ =8或
=8或 .
.
∵8>2π,舍去,∴ =
= .
.
(2)扇形的周长为40,∴ R+2R=40,
R+2R=40,
S= lR=
lR=
 R2=
R2=
 R·2R≤
R·2R≤
 .
.
当且仅当 R =2R,即R="10,"
R =2R,即R="10,"  =2时面积取得最大值,最大值为100.
=2时面积取得最大值,最大值为100.
 ,所对的弧长为l.
,所对的弧长为l.(1)依题意,得

∴2
 2-17
2-17 +8=0,∴
+8=0,∴ =8或
=8或 .
.∵8>2π,舍去,∴
 =
= .
.(2)扇形的周长为40,∴
 R+2R=40,
R+2R=40,S=
 lR=
lR=
 R2=
R2=
 R·2R≤
R·2R≤
 .
.当且仅当
 R =2R,即R="10,"
R =2R,即R="10,"  =2时面积取得最大值,最大值为100.
=2时面积取得最大值,最大值为100.
练习册系列答案
相关题目
 = 。
= 。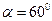 ,所在圆的半径R=10cm,则扇形的弧长= ;该弧所在的弓形的面积=
,所在圆的半径R=10cm,则扇形的弧长= ;该弧所在的弓形的面积=  的终边相同,那么
的终边相同,那么 的终边在 ( )
的终边在 ( ) 轴的非负半轴上
轴的非负半轴上 轴的非负半轴上
轴的非负半轴上 的值
的值 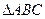 中,若
中,若 ,则
,则 ( )
( )


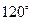
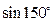 的值等于
的值等于



 的终边上的点
的终边上的点 与
与 关于
关于 轴对称
轴对称 ,角
,角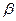 的终边上的点
的终边上的点 与
与 关于直线
关于直线 对称,求
对称,求 之值.
之值.