题目内容
已知函数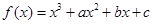 的图象如图,直线
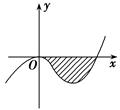
的图象如图,直线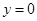 在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为
在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为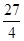 .
.
(1)求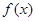 的解析式;
的解析式;
(2)若常数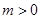 ,求函数
,求函数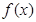 在区间
在区间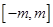 上的最大值.
上的最大值.
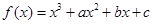 的图象如图,直线
的图象如图,直线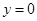 在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为
在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为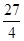 .
.
(1)求
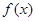 的解析式;
的解析式;(2)若常数
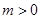 ,求函数
,求函数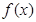 在区间
在区间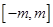 上的最大值.
上的最大值.(1) ;
;
(2)当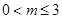 时,
时, ;当
;当 时,
时,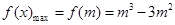 .
.
 ;
;(2)当
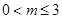 时,
时, ;当
;当 时,
时,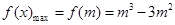 .
.试题分析:(1)由条件知,
 ,
, ,代入可得
,代入可得 、
、 .再用定积分表示出所围成的区域(阴影)面积,由面积为
.再用定积分表示出所围成的区域(阴影)面积,由面积为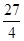 解得
解得 ,从而得到
,从而得到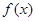 的解析式;(2)由(1)知
的解析式;(2)由(1)知 ,再列出
,再列出 ,的取值变化情况,又
,的取值变化情况,又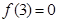 ,结合图像即可得当
,结合图像即可得当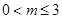 时,
时, ;当
;当 时,
时,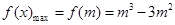 .
.试题解析:(1)由
 得
得 , 2分
, 2分 .由
.由 得
得 , 4分
, 4分∴
 ,则易知图中所围成的区域(阴影)面积为
,则易知图中所围成的区域(阴影)面积为
从而得
 ,∴
,∴ . 8分
. 8分(2)由(1)知
 .
. 的取值变化情况如下:
的取值变化情况如下:  |  |  |  | 2 |  |
 |  |  | 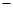 |  |  |
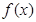 | 单调 递增 | 极大值 | 单调 递减 | 极小值 | 单调 递增 |
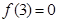 ,
,①当
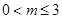 时,
时, ; 11分
; 11分②当
 时,
时,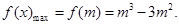
综上可知当
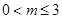 时,
时, ;当
;当 时,
时,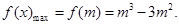

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
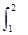 x2dx,S2=
x2dx,S2=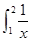 dx,S3=
dx,S3=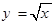 ,直线
,直线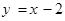 及
及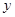 轴所围成的图形的面积为_______.
轴所围成的图形的面积为_______.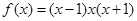 ,则满足
,则满足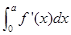 =0的实数a的有( )
=0的实数a的有( ) = .
= .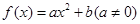 ,若
,若 ,则
,则 ( )
( )


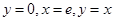 及曲线
及曲线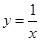 上的封闭的图形的面积为( )
上的封闭的图形的面积为( )
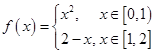 ,则
,则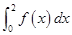 的值为( )
的值为( )



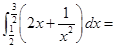 .
.