题目内容
(湖北卷文18)如图,在直三棱柱![]() 中,平面
中,平面![]() 侧面
侧面![]()
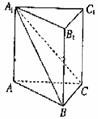 (Ⅰ)求证:
(Ⅰ)求证: ![]()
(Ⅱ)若![]() ,直线AC与平面
,直线AC与平面![]() 所成的角为
所成的角为![]() ,二面角
,二面角![]()
![]()
![]()
解:(Ⅰ)证明:如右图,过点A在平面A1ABB1内作AD⊥A1B于D,则
 由平面A1BC⊥侧面A1ABB1,且平面A1BC∩侧面A1ABB1=A1B,
由平面A1BC⊥侧面A1ABB1,且平面A1BC∩侧面A1ABB1=A1B,
得AD⊥平面
A1BC.又BC![]() 平面A1BC 所以AD⊥BC.
平面A1BC 所以AD⊥BC.
因为三棱柱ABC-A1B1C1是直三棱柱,则AA1⊥底面ABC,所以AA1⊥BC.
又AA1∩AD=A,从而BC⊥侧面A1ABB1,
又AB![]() 侧面A1ABB1,故AB⊥BC.
侧面A1ABB1,故AB⊥BC.
(Ⅱ)证法1:连接CD,则由(Ⅰ)知∠ACD就是直线AC与平面A1BC所成的角,∠ABA1就是二面角A1-BC-A的颊角,即∠ACD=θ,∠ABA1.=
于是在RtΔADC中,sinθ=![]() ,在RtΔADA1中,sin∠AA1D=
,在RtΔADA1中,sin∠AA1D=![]() ,
,
∴sinθ=sin∠AA1D,由于θ与∠AA1D都是锐角,所以θ=∠AA1D.
又由RtΔA1AB知,∠AA1D+=∠AA1B+=![]() ,故θ+=
,故θ+=![]() .
.
证法2:由(Ⅰ)知,以点B为坐标原点,以BC、BA、BB1所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
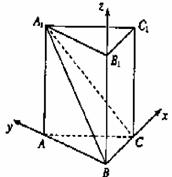 设AB=c(c<a=,则B(0,0,0),A(0,c,0),C(
设AB=c(c<a=,则B(0,0,0),A(0,c,0),C(![]() ),
),
A1(0,c,a),于是![]() ,
,![]() =(0,c,a),
=(0,c,a),
![]()
![]() c,a
c,a
设平面A1BC的一个法向量为n=(x,y,z),
则由
可取n=(0,-a,c),于是
n·![]() =ac>0,
=ac>0,![]() 与n的夹角为锐角,则与互为余角
与n的夹角为锐角,则与互为余角
==cossin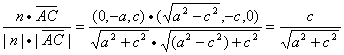 ,
,
=cos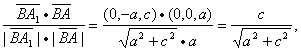
所以=sin(=cossin![]() ),又0<,<
),又0<,<![]() ,所以=+
,所以=+![]() .
.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 (Ⅰ)求证:
(Ⅰ)求证: