题目内容
已知条件p:5x>a+1或5x<1-a(a≥0)和条件q: >0,请选取适当的非负数a的值,分别利用所给的两个条件作为A,B构造命题:“若A,则B”,并使得构造的原命题为真命题,而其逆命题为假命题,则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
>0,请选取适当的非负数a的值,分别利用所给的两个条件作为A,B构造命题:“若A,则B”,并使得构造的原命题为真命题,而其逆命题为假命题,则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
【答案】分析:解P中的不等式组,我们可得x<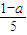 或x>
或x>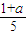 ,解q中的不等式我们可得x<
,解q中的不等式我们可得x< 或x>1,若要利用所给的两个条件作为A,B构造命题:“若A,则B”,并使得构造的原命题为真命题,而其逆命题为假命题,只需满足
或x>1,若要利用所给的两个条件作为A,B构造命题:“若A,则B”,并使得构造的原命题为真命题,而其逆命题为假命题,只需满足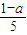 ≤
≤ ,且
,且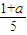 ≥1(端点等号不可同时取得)即可.
≥1(端点等号不可同时取得)即可.
解答:解:已知条件p:5x<-a+1或5x>a+1,
∴x<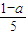 或x>
或x>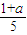 .
.
已知条件q,即2x2-3x+1>0,
∴x< 或x>1,
或x>1,
令a=4,则p:x<-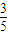 或x>1,
或x>1,
此时必有p⇒q成立,反之不然.
故可以选取的一个非负实数是a=4.
A为p,B为q,对应的命题是若p则q.
自以上过程可知这一命题的原命题为真命题,但它的逆命题为假命题.
点评:本题考查的知识点是四种命题的真假判断,及充要条件的性质,若要利用所给的两个条件作为A,B构造命题:“若A,则B”,并使得构造的原命题为真命题,而其逆命题为假命题,则A为B的充分不必要的条件,根据谁小谁充分的原则,我们可得A?B
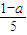 或x>
或x>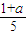 ,解q中的不等式我们可得x<
,解q中的不等式我们可得x< 或x>1,若要利用所给的两个条件作为A,B构造命题:“若A,则B”,并使得构造的原命题为真命题,而其逆命题为假命题,只需满足
或x>1,若要利用所给的两个条件作为A,B构造命题:“若A,则B”,并使得构造的原命题为真命题,而其逆命题为假命题,只需满足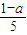 ≤
≤ ,且
,且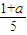 ≥1(端点等号不可同时取得)即可.
≥1(端点等号不可同时取得)即可.解答:解:已知条件p:5x<-a+1或5x>a+1,
∴x<
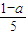 或x>
或x>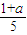 .
.已知条件q,即2x2-3x+1>0,
∴x<
 或x>1,
或x>1,令a=4,则p:x<-
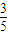 或x>1,
或x>1,此时必有p⇒q成立,反之不然.
故可以选取的一个非负实数是a=4.
A为p,B为q,对应的命题是若p则q.
自以上过程可知这一命题的原命题为真命题,但它的逆命题为假命题.
点评:本题考查的知识点是四种命题的真假判断,及充要条件的性质,若要利用所给的两个条件作为A,B构造命题:“若A,则B”,并使得构造的原命题为真命题,而其逆命题为假命题,则A为B的充分不必要的条件,根据谁小谁充分的原则,我们可得A?B

练习册系列答案
相关题目
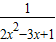 >0,请选取适当的非负数a的值,分别利用所给的两个条件作为A,B构造命题:“若A,则B”,并使得构造的原命题为真命题,而其逆命题为假命题,则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
>0,请选取适当的非负数a的值,分别利用所给的两个条件作为A,B构造命题:“若A,则B”,并使得构造的原命题为真命题,而其逆命题为假命题,则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.